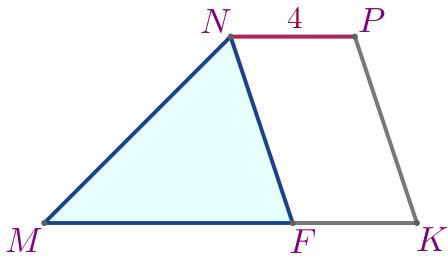
В трапеции \(\displaystyle MNPK\) большее основание \(\displaystyle MK{\small.}\) Через вершину \(\displaystyle N\) проведена прямая, параллельная стороне \(\displaystyle PK{\small,}\) до пересечения с основанием \(\displaystyle MK\) в точке \(\displaystyle F{\small.}\) Периметр треугольника \(\displaystyle MNF\) равен \(\displaystyle 20\, \footnotesize см {\small,}\) а \(\displaystyle BC=4\, \footnotesize см {\small.}\) Найдите периметр трапеции.
\(\displaystyle P_{MNPK}=\) \(\displaystyle \footnotesize см{\small.}\)
 |
Требуется найти периметр данной трапеции. |
Периметр многоугольника равен сумме длин всех его сторон. Тогда
\(\displaystyle P_{MNPK}=MN+NP+PK+MK=\color{red}{\large?}\)
\(\displaystyle P_{\triangle MNF}=\color{blue}{MN}+\color{blue}{NF}+\color{blue}{MF}=20\, \footnotesize см{\small.}\)
| 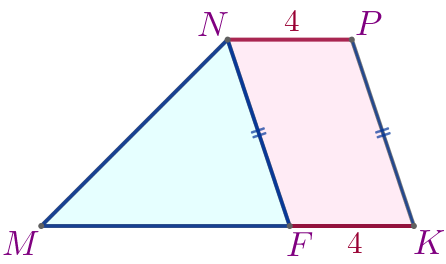 |
В четырёхугольнике \(\displaystyle NPKF\) противоположные стороны попарно параллельны.
Следовательно, \(\displaystyle NPKF\) – параллелограмм по определению. Тогда
\(\displaystyle FK=NP=4\, \footnotesize см{\small;}\)
\(\displaystyle PK=\color{blue}{NF}{\small.}\)
Так как точка \(\displaystyle F\) лежит на основании трапеции \(\displaystyle MK{\small,}\) то
\(\displaystyle MK=\color{blue}{MF}+FK=\color{blue}{MF}+4{\small.}\)
Подставим в формулу периметра трапеции \(\displaystyle NP=4 {\small,}\) \(\displaystyle PK=\color{blue}{NF}\) и \(\displaystyle MK=\color{blue}{MF}+4{\small.}\)
\(\displaystyle\begin{aligned}P_{MNPK}&=MN+NP+PK+MK=\\&=\color{blue}{MN}+4+\color{blue}{NF}+\color{blue}{MF}+4=\\&=\underset{P_{\triangle MNF}}{\underbrace{\color{blue}{MN}+\color{blue}{NF}+\color{blue}{MF}}}+8=20+8=28\, \footnotesize см{\small.}\end{aligned}\)
Ответ: \(\displaystyle P_{MNPK}=28\, \footnotesize см{\small.}\)