В треугольнике \(\displaystyle ABC\) медиана \(\displaystyle AM\) продолжена за точку \(\displaystyle M\) на расстояние, равное \(\displaystyle AM{\small.}\) Найдите расстояние от полученной точки до вершины \(\displaystyle B{\small,}\) если \(\displaystyle AB=6{\small,}\) \(\displaystyle AC=8{\small.}\)
По условию задачи выполним построение.
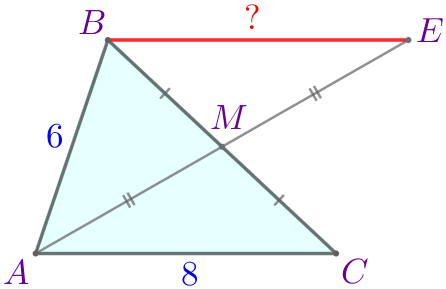 | \(\displaystyle ABC\) – треугольник:
Требуется найти расстояние \(\displaystyle BE{\small.}\) |
Соединим точки \(\displaystyle C\) и \(\displaystyle E\) отрезком. Получили четырёхугольник \(\displaystyle ABEC{\small,}\) в котором:
| 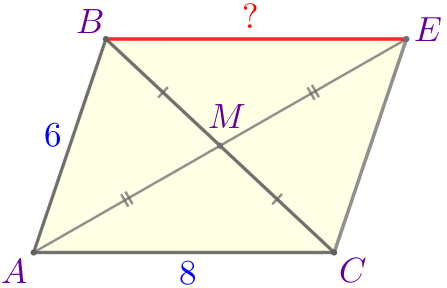 |
То есть в четырёхугольнике \(\displaystyle ABEC\) диагонали точкой пересечения делятся пополам.
Следовательно, по признаку параллелограмма
\(\displaystyle ABEC\) – параллелограмм.
В параллелограмме противоположные стороны равны. Значит,
\(\displaystyle BE=AC=8{\small.}\)
Ответ: \(\displaystyle 8{\small.}\)