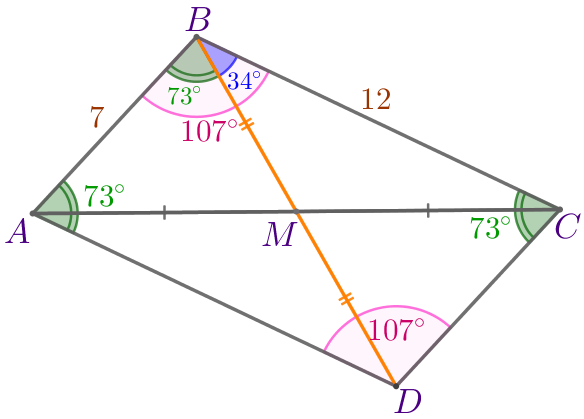
Найдите длину медианы \(\displaystyle BM\) треугольника \(\displaystyle ABC{\small,}\) если известно, что \(\displaystyle AB=7{\small,}\) \(\displaystyle BC=12{\small,}\) \(\displaystyle \angle ABM=73^{\circ}\) и \(\displaystyle \angle CBM=34^{\circ}{\small.}\)
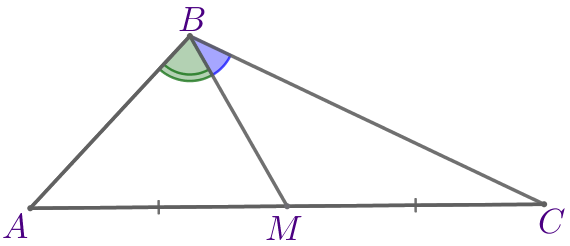
\(\displaystyle BM=\)
Отметим на рисунке известные величины.
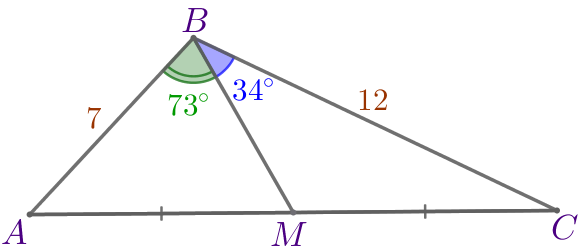 | \(\displaystyle ABC\) – треугольник:
|
Требуется найти длину медианы \(\displaystyle BM{\small.}\)
Продлим медиану \(\displaystyle BM\) за точку \(\displaystyle M\) и отметим точку \(\displaystyle D\) так, что \(\displaystyle BM=MD{\small.}\) Получили четырёхугольник \(\displaystyle ABCD{\small,}\) в котором:
| 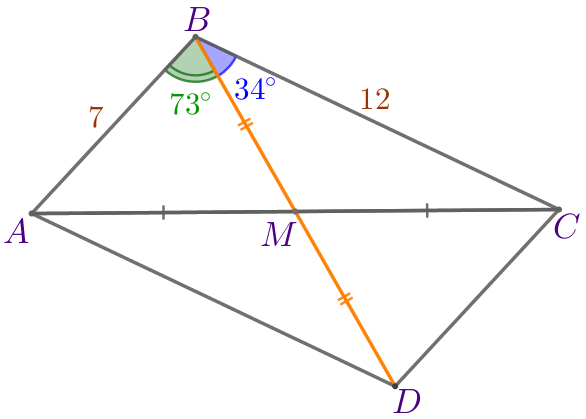 |
То есть в четырёхугольнике \(\displaystyle ABCD\) диагонали точкой пересечения делятся пополам.
\(\displaystyle ABCD\) – параллелограмм.
\(\displaystyle \angle B=\angle ABD+\angle CBD=73^{\circ}+34^{\circ}=107^{\circ}{\small.}\)
|
\(\displaystyle \angle C=180^{\circ}-\angle B=180^{\circ}-107^{\circ}=73^{\circ}{\small.}\)
\(\displaystyle \angle D= \angle B=107^{\circ}{\small;}\) \(\displaystyle \angle A= \angle C=73^{\circ}{\small.}\) |
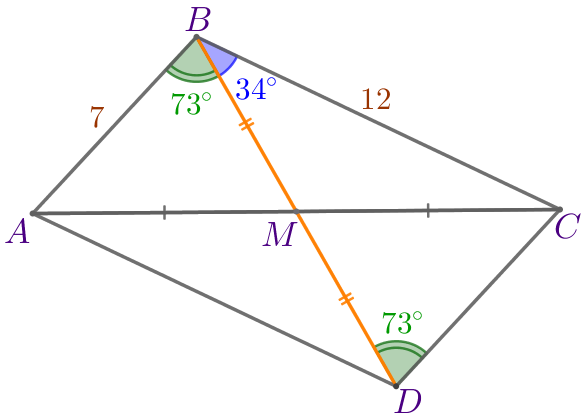 | В параллелограмме противоположные стороны попарно параллельны. Тогда \(\displaystyle \angle BDC=\angle ABD\) как накрест лежащие при параллельных прямых \(\displaystyle AB\) и \(\displaystyle CD\) и секущей \(\displaystyle BD{\small.}\) То есть \(\displaystyle \angle BDC=73^{\circ}{\small.}\) |
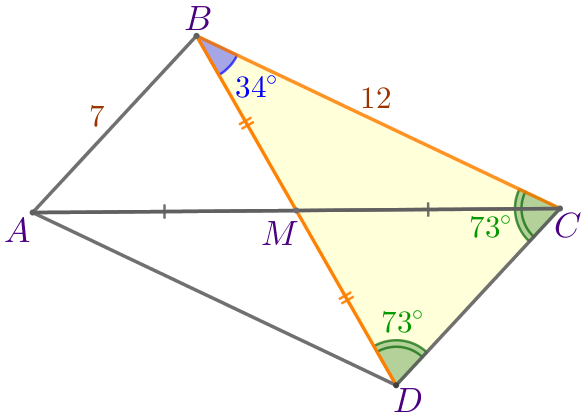 | Так как \(\displaystyle \angle BCD=\angle BDC=73^{\circ}{\small,}\) то \(\displaystyle \triangle BCD\) – равнобедренный. Значит, \(\displaystyle BD=BC=12{\small.}\) По построению \(\displaystyle BM=MD{\small,}\) следовательно, \(\displaystyle BM=\frac{1}{2}\cdot BD=\frac{1}{2} \cdot 12=6{\small.}\) |
Ответ: \(\displaystyle BM=6{\small.}\)