В треугольнике \(\displaystyle ABC\) медиана \(\displaystyle BM\) равна половине стороны \(\displaystyle AC{\small.}\) Найдите величину угла \(\displaystyle ABC{\small.}\)
\(\displaystyle \angle ABC=\)\(\displaystyle ^{\circ}{\small.}\)
По условию задачи сделаем чертёж.
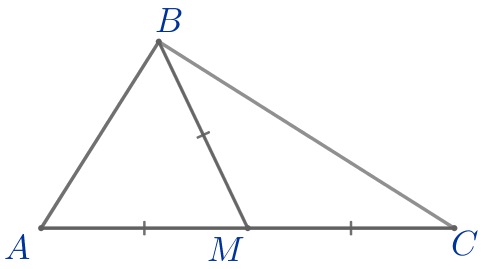 | \(\displaystyle ABC\) – треугольник:
Требуется найти величину угла \(\displaystyle ABC{\small.}\) |
Выполним дополнительное построение. Продлим медиану \(\displaystyle BM\) за точку \(\displaystyle M\) и отметим точку \(\displaystyle D\) так, что \(\displaystyle BM=MD{\small.}\) Получили четырёхугольник \(\displaystyle ABCD{\small,}\) в котором \(\displaystyle AM=MC=BM=MD{\small.}\) То есть в четырёхугольнике \(\displaystyle ABCD\) диагонали равны и точкой пересечения делятся пополам. | 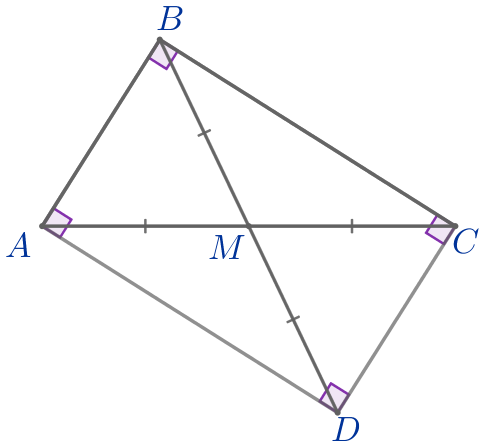 |
Следовательно, по признаку прямоугольника
\(\displaystyle ABCD\) – прямоугольник.
В результате получаем
\(\displaystyle \angle ABC=90^{\circ}{\small.}\)
Ответ: \(\displaystyle \angle ABC=90^{\circ}{\small.}\)