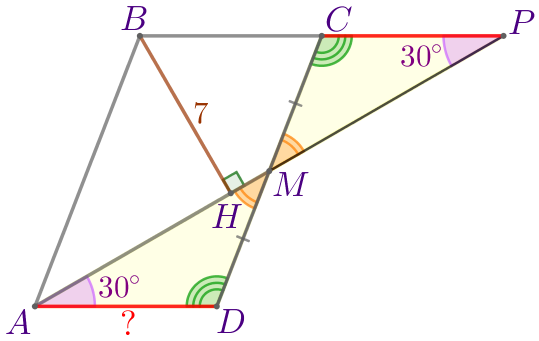
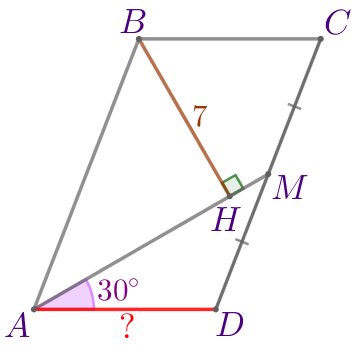
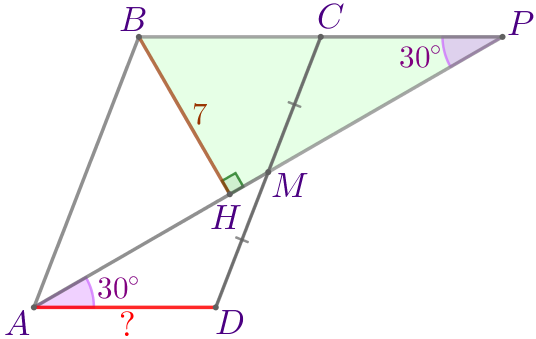
Точка \(\displaystyle M\) – середина стороны \(\displaystyle CD\) параллелограмма \(\displaystyle ABCD{\small.}\) Расстояние от вершины \(\displaystyle B\) данного параллелограмма до прямой \(\displaystyle AM\) равно \(\displaystyle 7{\small.}\) Найдите длину стороны \(\displaystyle AD{\small,}\) если известно, что \(\displaystyle \angle MAD=30^{\circ}{\small.}\)
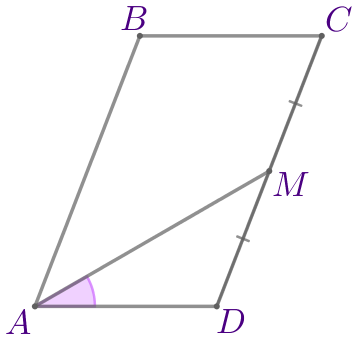
\(\displaystyle AD=\)
 | \(\displaystyle ABCD\) – параллелограмм:
Требуется найти длину стороны \(\displaystyle AD{\small.}\) |
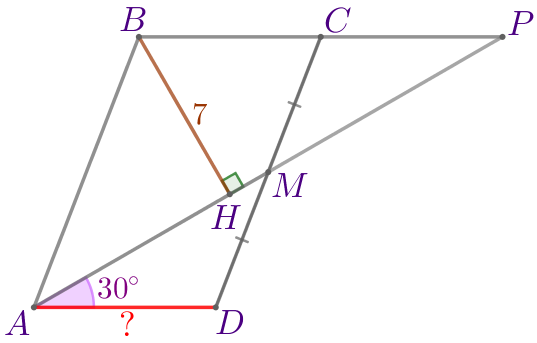 | Продлим отрезок \(\displaystyle AM\) за точку \(\displaystyle M\) до пересечения с прямой \(\displaystyle BC{\small.}\) \(\displaystyle P\) – точка пересечения прямых \(\displaystyle AM\) и \(\displaystyle BC{\small.}\) |
|
Следовательно, \(\displaystyle \triangle PCM=\triangle ADM\) по стороне и двум прилежащим углам. |
Значит,
\(\displaystyle \angle MPC=\angle MAD=30^{\circ}{\small;}\)
\(\displaystyle CP=AD{\small.}\)
 |
В прямоугольном треугольнике против угла \(\displaystyle 30^{\circ}\) лежит катет, равный половине гипотенузы. То есть \(\displaystyle BH=\frac{1}{2}BP{\small.}\) Значит, \(\displaystyle BP=2 \cdot BH=2 \cdot 7=14{\small.}\) |
Так как точка \(\displaystyle C\) лежит на отрезке \(\displaystyle BP{\small,}\) то
\(\displaystyle BP=BC+CP{\small.}\)
Подставим
- \(\displaystyle BP=14{\small;}\)
- \(\displaystyle BC=AD\) – противоположные стороны параллелограмма;
- \(\displaystyle CP=AD\) – соответственные стороны в равных треугольниках.
В результате получаем
\(\displaystyle 14=AD+AD{\small;}\)
\(\displaystyle 2 \cdot AD=14{\small;}\)
\(\displaystyle AD=7{\small.}\)
Ответ: \(\displaystyle AD=7{\small.}\)