Стороны треугольника \(\displaystyle ABC\) относятся как \(\displaystyle 4:5:7{\small.}\) Найдите стороны подобного ему треугольника \(\displaystyle A_1B_1C_1{\small,}\) если периметр треугольника \(\displaystyle A_1B_1C_1\) равен \(\displaystyle 96{\small.}\)
\(\displaystyle {\small;}\) \(\displaystyle {\small;}\) \(\displaystyle {\small.}\)
Пусть в треугольнике \(\displaystyle ABC\) \(\displaystyle AB:BC:AC=4:5:7{\small,}\) тогда для сходственных сторон подобного треугольника \(\displaystyle A_1B_1C_1\) выполняется такое же соотношение:
\(\displaystyle A_1B_1:B_1C_1:A_1C_1=4:5:7{\small.}\)
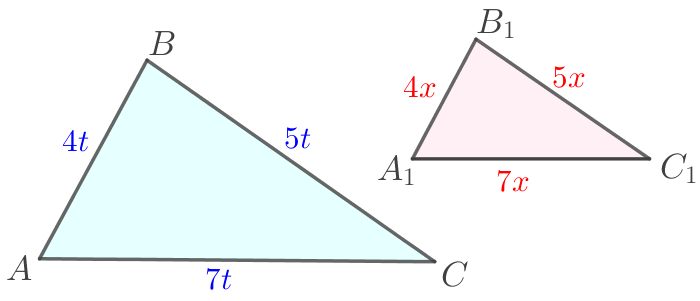 | Значит, \(\displaystyle A_1B_1=4x{\small;}\) \(\displaystyle B_1C_1=5x{\small;}\) \(\displaystyle A_1C_1=7x{\small.}\) |
Периметр треугольника равен сумме длин всех его сторон:
\(\displaystyle P_{\triangle A_1B_1C_1}=A_1B_1+B_1C_1+A_1C_1{\small;}\)
\(\displaystyle P_{\triangle A_1B_1C_1}=4x+5x+7x=16x{\small.}\)
По условию \(\displaystyle P_{\triangle A_1B_1C_1}=96{\small,}\) то есть
\(\displaystyle 16x=96{\small;}\)
\(\displaystyle x=6{\small.}\)
Тогда
\(\displaystyle A_1B_1=4x=4 \cdot 6=24{\small;}\)
\(\displaystyle B_1C_1=5x=5 \cdot 6=30{\small;}\)
\(\displaystyle A_1C_1=7x=7 \cdot 6=42{\small.}\)
Стороны подобного треугольника \(\displaystyle A_1B_1C_1\) равны \(\displaystyle 24{\small,}\) \(\displaystyle 30\) и \(\displaystyle 42{\small.}\)
Ответ: \(\displaystyle 24{\small;}\) \(\displaystyle 30{\small;}\) \(\displaystyle 42{\small.}\)