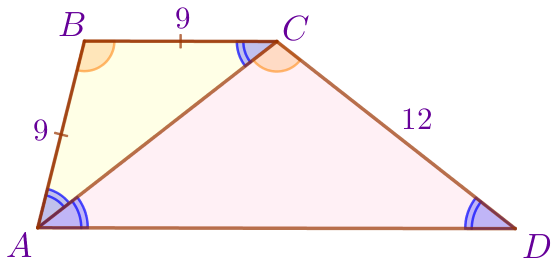
В трапеции \(\displaystyle ABCD\) \(\displaystyle (AD \parallel BC ) \) \(\displaystyle AC\) – биссектриса угла \(\displaystyle A\) делит трапецию на два подобных треугольника \(\displaystyle ABC\) и \(\displaystyle ACD{\small,}\) \(\displaystyle AB=9\, {\footnotesize см}{\small,}\) \(\displaystyle CD=12\, {\footnotesize см}{\small.}\) Найдите периметр трапеции.
\(\displaystyle P_{ABCD}=\)\(\displaystyle {\footnotesize см}{\small.}\)
 | \(\displaystyle ABCD\) – трапеция:
|
Требуется найти периметр трапеции \(\displaystyle ABCD{\small.}\)
Периметр трапеции равен сумме длин всех её сторон:
\(\displaystyle P_{ABCD}=AB+BC+CD+AD{\small.}\)
\(\displaystyle BC=9{\small.}\)
 |
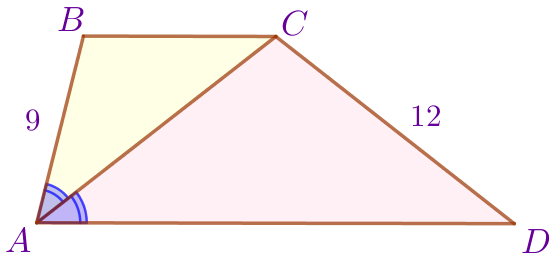
\(\displaystyle \color{blue}{\angle BAC}= \color{blue}{\angle CAD}{\small;}\)
\(\displaystyle \color{blue}{\angle BCA}= \color{blue}{\angle CAD}\) (накрест лежащие) |
Следовательно, \(\displaystyle \color{blue}{\angle BAC}=\color{blue}{ \angle BCA} \) и \(\displaystyle \triangle ABC\) – равнобедренный. Тогда
\(\displaystyle BC=AB=9\, {\footnotesize см}{\small.}\)
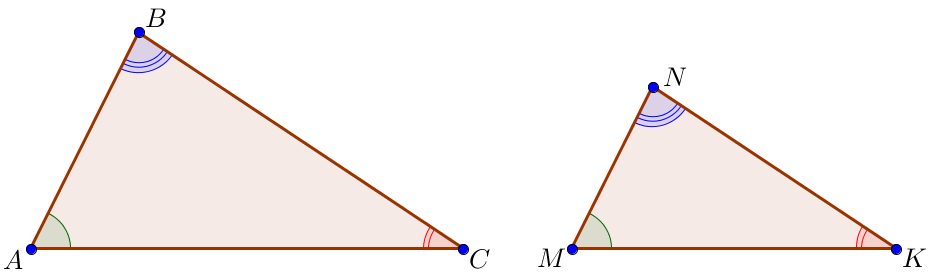
Определим соответственно равные углы этих треугольников.
\(\displaystyle \angle BCA= \angle CAD{\small;}\) \(\displaystyle \angle BAC= \angle ADC{\small;}\) \(\displaystyle \angle ABC= \angle ACD{\small.}\)
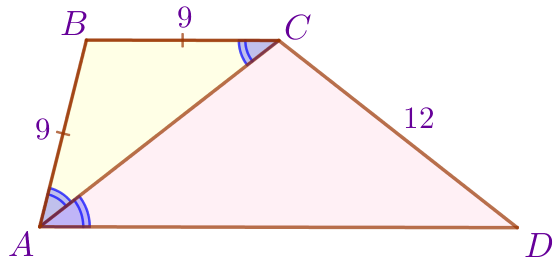
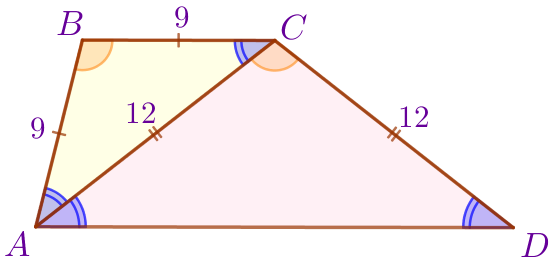 | Треугольник \(\displaystyle ACD\) равнобедренный, значит, \(\displaystyle AC=CD=12\, {\footnotesize см}{\small.}\) |
В подобных треугольниках сходственные стороны лежат напротив соответственно равных углов.
Следовательно,
\(\displaystyle \frac{AB}{CD}=\frac{BC}{AC}=\frac{AC}{AD}{\small.}\)
Из равенства \(\displaystyle \frac{BC}{AC}=\frac{AC}{AD}\) по пропорции выразим \(\displaystyle AD{\small:}\)
\(\displaystyle AD=\frac{AC \cdot AC}{BC}{\small.}\)
Подставим \(\displaystyle AC=12\, {\footnotesize см}{\small,}\) \(\displaystyle BC=9\, {\footnotesize см}{\small:}\)
\(\displaystyle AD=\frac{12 \cdot 12}{9}=\frac{144}{9}=16\, {\footnotesize см}{\small.}\)
Найдём периметр трапеции:
\(\displaystyle P_{ABCD}=AB+BC+CD+AD=9+9+12+16=46\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle P_{ABCD}=46\, {\footnotesize см}{\small.}\)