Одна из сторон параллелограмма равна \(\displaystyle 5 \small,\) а площадь параллелограмма равна \(\displaystyle 30 \small.\) Найдите высоту, опущенную на эту сторону.
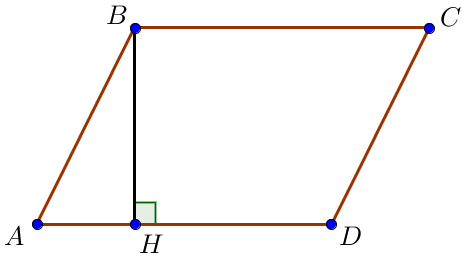
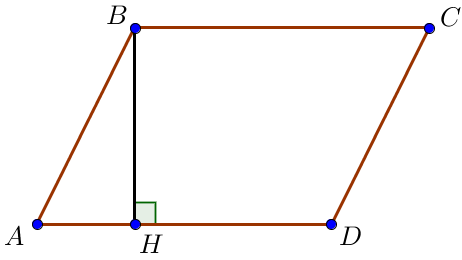
Пусть сторона параллелограмма \(\displaystyle AD=5 {\small .}\) Требуется найти высоту \(\displaystyle BH {\small .}\)
Воспользуемся одной из формул для вычисления площади параллелограмма.
Формула площади параллелограмма
\(\displaystyle S=h\cdot a_h \small,\)
где \(\displaystyle h\) – высота параллелограмма,
\(\displaystyle a_h \) – основание параллелограмма, к которому проведена высота.
В данном случае площадь параллелограмма равна произведению высоты \(\displaystyle BH\) на основание \(\displaystyle AD{\small : } \)
\(\displaystyle {S_{пар}} = {BH }\cdot AD {\small.}\)
Тогда
\(\displaystyle {30} = {BH }\cdot 5 {\small ,}\)
\(\displaystyle {BH }= \frac{30}{5}=6 {\small.}\)
Ответ: \(\displaystyle 6 {\small .}\)