Биссектрисы углов \(\displaystyle A\) и \(\displaystyle B\) параллелограмма \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle K{\small.}\) Найдите площадь параллелограмма, если \(\displaystyle BC=11 {\small,}\) а расстояние от точки \(\displaystyle K\) до стороны \(\displaystyle AB\) равно \(\displaystyle 3 {\small.}\)
По условию задачи выполним чертёж.
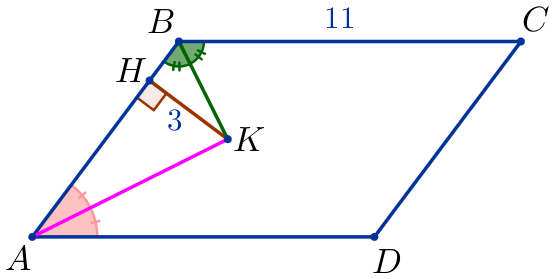 | \(\displaystyle ABCD\) – параллелограмм, \(\displaystyle BC=11{\small,}\) \(\displaystyle BK\) – биссектриса угла \(\displaystyle ABC{\small,}\) \(\displaystyle AK\) – биссектриса угла \(\displaystyle BAD{\small,}\) \(\displaystyle KH=3\)– расстояние от точки \(\displaystyle K\) до стороны \(\displaystyle AB{\small.}\) |
Требуется найти площадь параллелограмма \(\displaystyle ABCD{\small.}\)
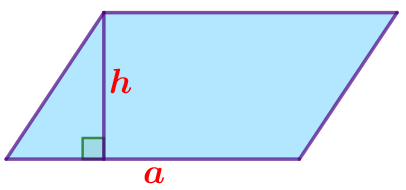
\(\displaystyle S_{ABCD}=BC \cdot h{\small,}\) где \(\displaystyle h\) – высота параллелограмма.
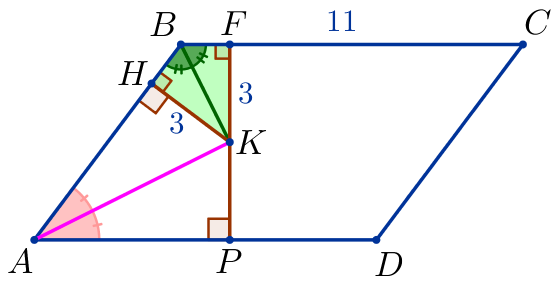
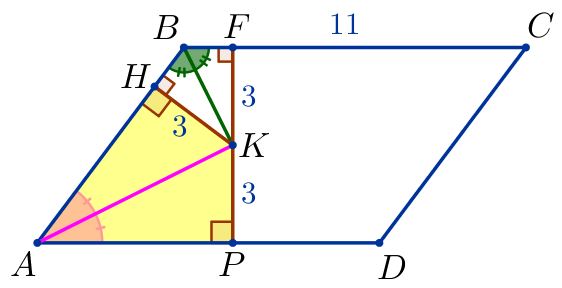
Через точку \(\displaystyle K\) построим высоту \(\displaystyle FP\) параллелограмма \(\displaystyle ABCD{\small.}\) | 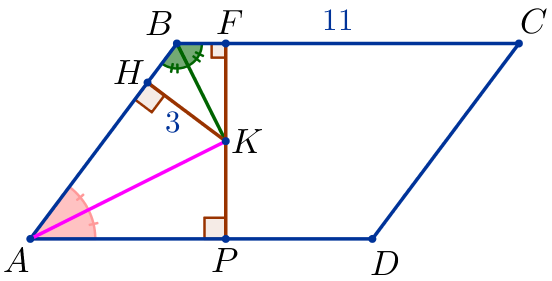 |
\(\displaystyle FP=6 {\small.}\)
Получаем
\(\displaystyle S_{ABCD}=BC \cdot FP{\small,}\)
\(\displaystyle S_{ABCD}=11 \cdot 6=66 {\small.}\)
Ответ: \(\displaystyle 66{\small.}\)