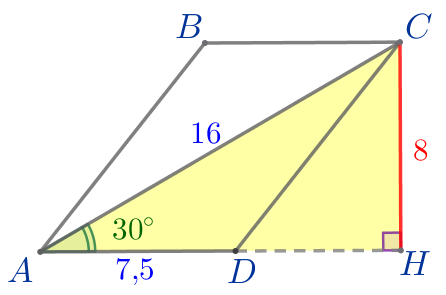
Сторона параллелограмма равна \(\displaystyle 7{,}5\, {\footnotesize см}{\small,}\) а диагональ, равная \(\displaystyle 16\, {\footnotesize см}{\small,}\) образует с ней угол \(\displaystyle 30^{\circ}{\small.}\) Найдите площадь параллелограмма.
\(\displaystyle {\footnotesize см^2}{\small.}\)
По условию задачи построим чертёж.
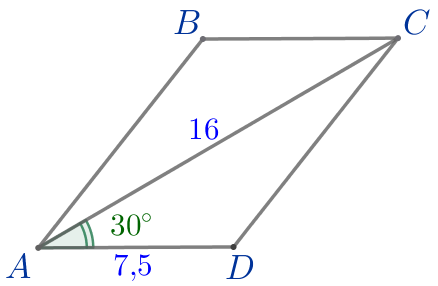 | \(\displaystyle ABCD\) – параллелограмм:
Требуется найти площадь параллелограмма \(\displaystyle ABCD{\small.}\) |
\(\displaystyle S_{ABCD}=AD \cdot h{\small,}\) где \(\displaystyle h\) – высота параллелограмма.
Выполним дополнительное построение.
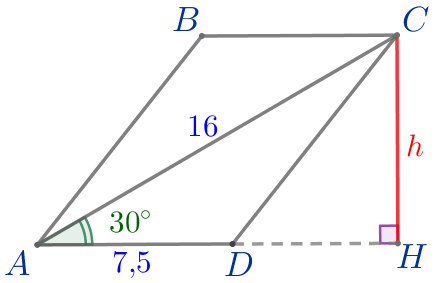 | Из вершины \(\displaystyle C\) к продолжению стороны \(\displaystyle AD\) проведем высоту \(\displaystyle CH=\color{red}{h}{\small.}\) |
\(\displaystyle \color{red}{h}=8{\small.}\)
Подставим в формулу площади \(\displaystyle AD=7{,}5\) и \(\displaystyle h=8{\small:}\)
\(\displaystyle S_{ABCD}=AD \cdot h=7{,}5 \cdot 8=60{\small.}\)
Ответ: \(\displaystyle 60\, {\footnotesize см^2}{\small.}\)