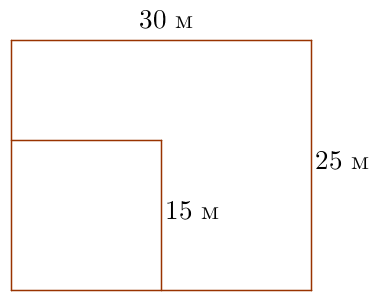
Дачный участок имеет форму прямоугольника со сторонами \(\displaystyle 25 \) метров и \(\displaystyle 30\) метров. Хозяин отгородил на участке квадратный вольер со стороной \(\displaystyle 15\)м (см. рис.). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
Площадь участка найдем по формуле площади прямоугольника
\(\displaystyle S=a \cdot b\small, \)
где \(\displaystyle a\) и \(\displaystyle b\) – длины смежных сторон прямоугольника.
Стороны участка равны \(\displaystyle a=30\)м, \(\displaystyle b=25\)м. Значит,
\(\displaystyle S_{\scriptsize{участка}}=30\cdot 25= 750\)(кв.м)
Площадь квадратного вольера найдем по формуле площади квадрата
\(\displaystyle S=с^{2}\small, \)
где \(\displaystyle с=15\) – длина стороны квадрата.
Значит,
\(\displaystyle S_{\scriptsize{вольера}}=15^2= 225\)(кв.м)
Чтобы найти площадь оставшейся части участка, вычтем из площади всего участка площадь, занятую вольером. То есть
\(\displaystyle S_{\scriptsize{остав.\ части\ участка}}=S_{\scriptsize{участка}}-S_{\scriptsize{вольера}} \small,\)
\(\displaystyle S_{\scriptsize{остав.\ части\ участка}}=750-225=525\)(кв.м)
Ответ: \(\displaystyle 525 \small. \)