Один из углов параллелограмма равен \(\displaystyle \alpha\small.\) Внутри параллелограмма отметили точку \(\displaystyle X\) и получили четыре проекции точки \(\displaystyle X\) на все стороны параллелограмма: \(\displaystyle Y_1,\,Y_2,\,Y_3\) и \(\displaystyle Y_4\small.\) Найдите отношение площади исходного параллелограмма к площади \(\displaystyle Y_1Y_2Y_3Y_4{\small:}\)
Так как противоположные стороны параллелограмма параллельны, то отрезки \(\displaystyle Y_1X\) и \(\displaystyle Y_3X\) составляют одну прямую. Также точки \(\displaystyle Y_2,\,X,\,Y_4\) лежат на одной прямой. | 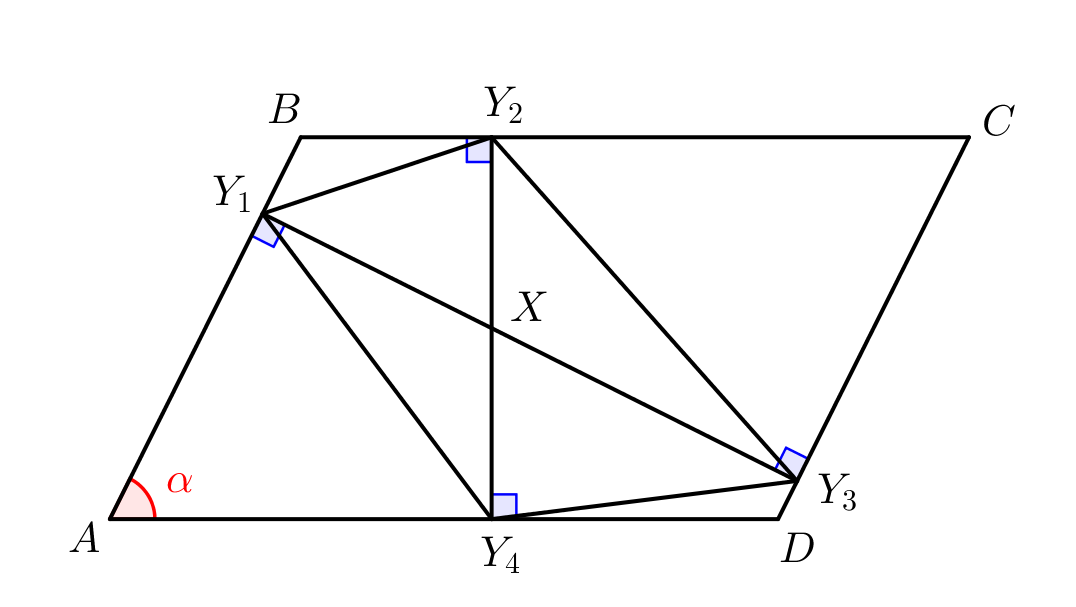 |
Чтобы решить задачу:
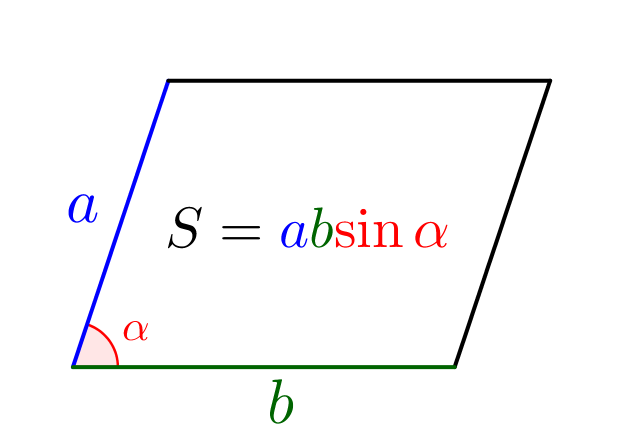
- выразим площадь параллелограмма через стороны и угол \(\displaystyle \alpha\small,\)
- выразим площадь \(\displaystyle Y_1Y_2Y_3Y_4\) через произведение диагоней и синус угла между ними,
- выразим диагонали \(\displaystyle Y_1Y_2Y_3Y_4\) через стороны параллелограмма.
\(\displaystyle S_{ABCD}=AB\cdot AD\cdot\sin\alpha\small.\)
\(\displaystyle S_{Y_1Y_2Y_3Y_4}=\frac{Y_1Y_3\cdot Y_2Y_4\cdot\sin\alpha}{2}\small.\)
Найдем угол между диагоналями \(\displaystyle Y_1Y_2Y_3Y_4\small.\) Рассмотрим четырехугольник \(\displaystyle AY_1XY_4\small.\) Три его угла известны: \(\displaystyle \angle A=\alpha,\,\angle Y_1=90^{\circ}\) и \(\displaystyle \angle Y_4=90^{\circ}\small.\) Так как сумма углов четырехугольника равна \(\displaystyle 360^{\circ}\small,\) то последний угол: \(\displaystyle \angle Y_1XY_4=360^{\circ}-\alpha-90^{\circ}-90^{\circ}=180-\alpha\small.\) | 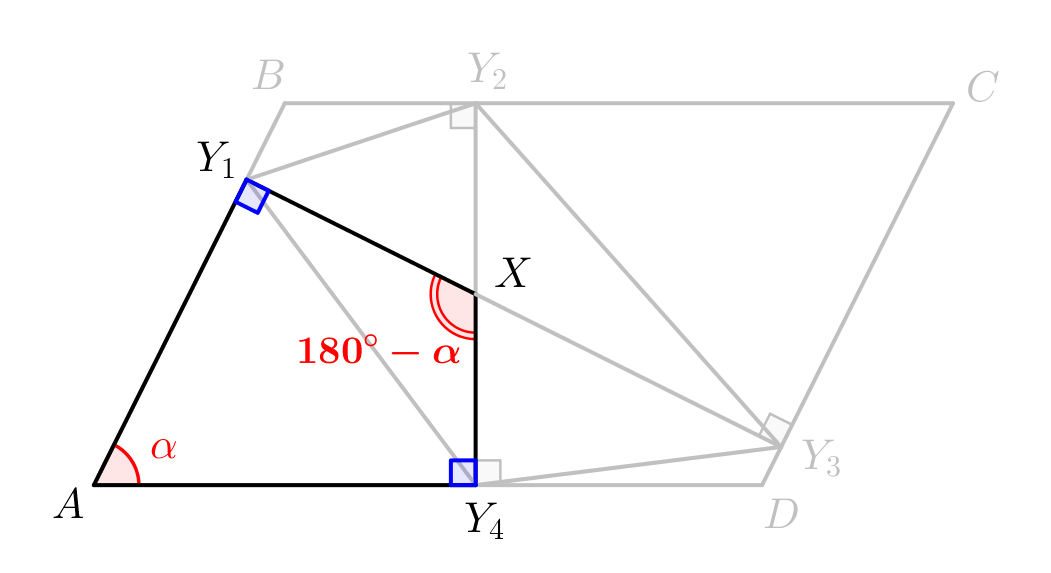 |
Теперь воспользуемся формулой для вычисления площади четырехугольника:
Формула площади четырёхугольника через его диагонали и угол между ними
Площадь четырехугольника с диагоналями \(\displaystyle d_1,\,d_2\) и углом \(\displaystyle \color{red}{\alpha}\) между ними равна \(\displaystyle \frac{1}{2}d_1d_2\sin\color{red}{\alpha}\small.\)

Тогда \(\displaystyle S_{Y_1Y_2Y_3Y_4}=\frac{Y_1Y_3\cdot Y_2Y_4\cdot\sin(180^{\circ}-\alpha)}{2}\small.\) Согласно формуле приведения \(\displaystyle \sin(180^{\circ}-\alpha)=\sin\alpha\small,\) тогда \(\displaystyle S_{Y_1Y_2Y_3Y_4}=\frac{Y_1Y_3\cdot Y_2Y_4\cdot\sin\alpha}{2}\small.\) | 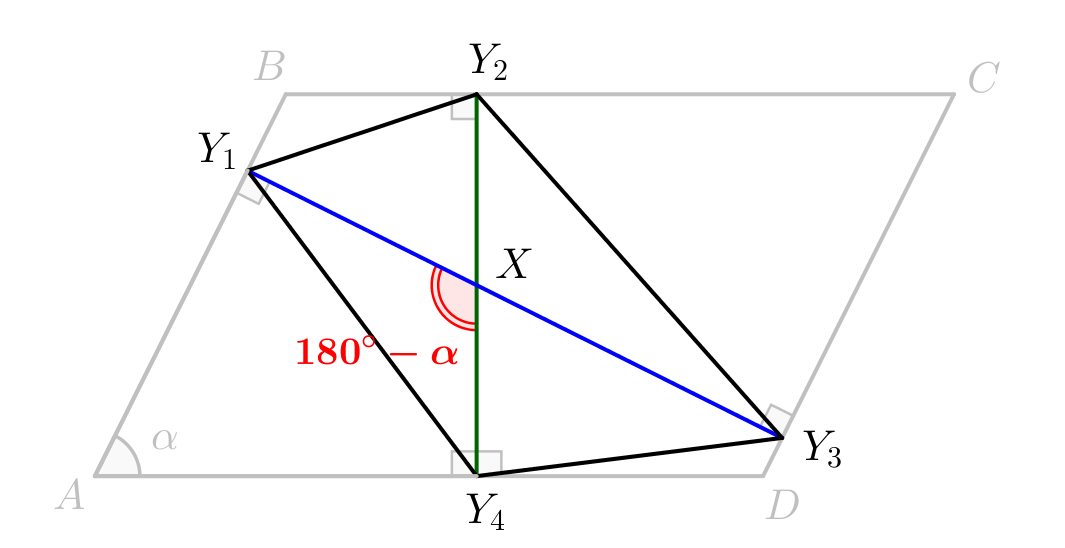 |
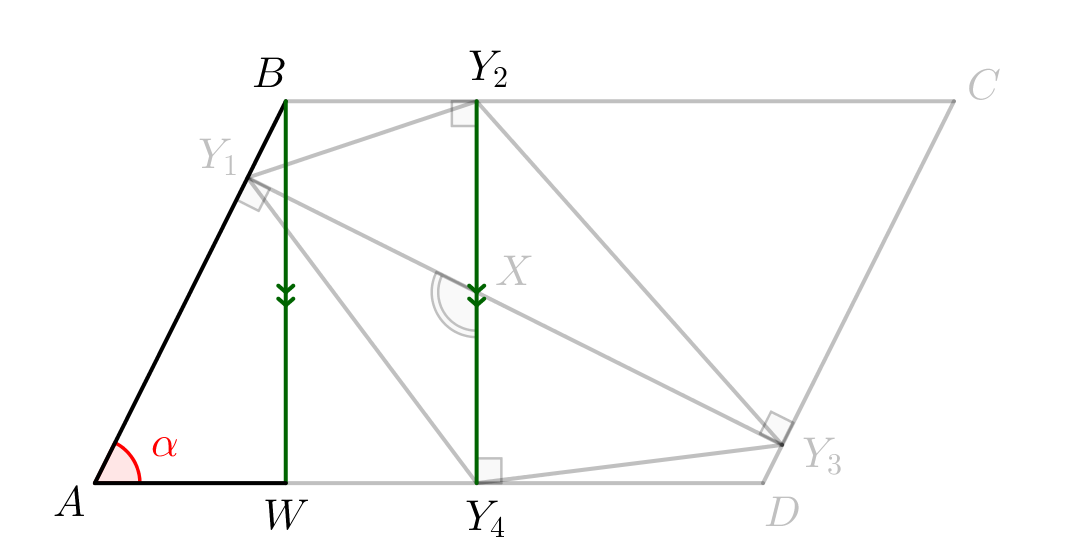
\(\displaystyle Y_1Y_3=AD\sin\alpha\small.\)
Отрезок \(\displaystyle Y_1Y_3\) является одной из высот параллелограмма. Проведем отрезок \(\displaystyle DZ\) – параллельный \(\displaystyle Y_1Y_3\small.\) Противоположные стороны \(\displaystyle DZY_1Y_3\) параллельны, то есть \(\displaystyle DZY_1Y_3\) – параллелограмм и \(\displaystyle DZ=Y_1Y_3\small.\) Рассмотрим прямоугольный треугольник \(\displaystyle DAZ\small.\) В нем \(\displaystyle DZ=AD\sin\alpha\small.\) Значит, \(\displaystyle Y_1Y_3=DZ=AD\sin\alpha\small.\) | 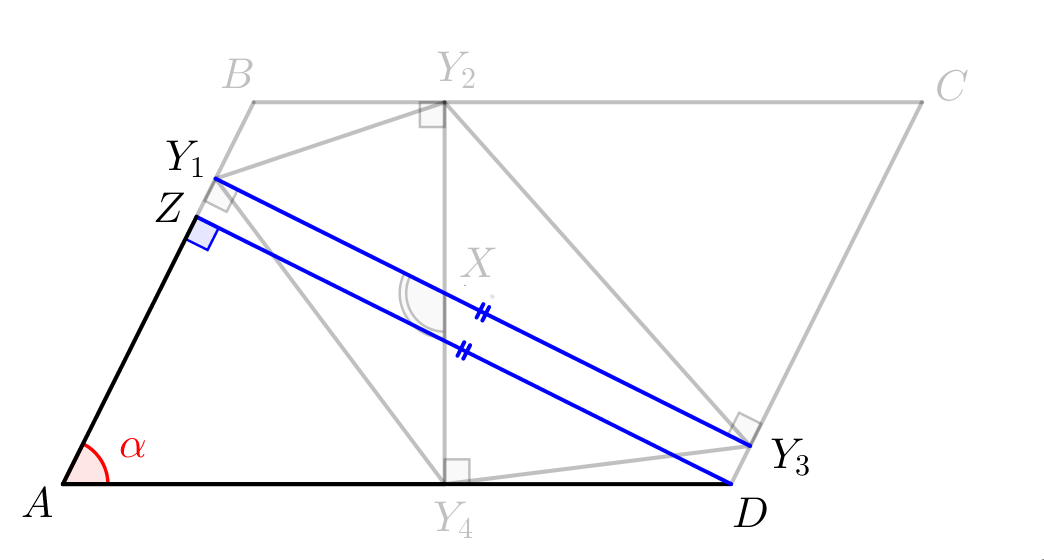 |
\(\displaystyle Y_2Y_4=AB\sin\alpha\small.\)
Отношение площадей равно:
\(\displaystyle \frac{S_{ABCD}}{S_{Y_1Y_2Y_3Y_4}}=\frac{AB\cdot AD\cdot\sin\alpha}{\frac{Y_1Y_3\cdot Y_2Y_4\cdot\sin\alpha}{2}}=\frac{2AB\cdot AD}{Y_1Y_3\cdot Y_2Y_4}\small.\)
Подставим диагонали \(\displaystyle Y_1Y_3=AD\sin\alpha\) и \(\displaystyle Y_2Y_4=AB\sin\alpha{\small:}\)
\(\displaystyle \frac{S_{ABCD}}{S_{Y_1Y_2Y_3Y_4}}=\frac{2AB\cdot AD}{Y_1Y_3\cdot Y_2Y_4}=\frac{2AB\cdot AD}{AD\sin\alpha\cdot AB\sin\alpha}=\frac{2}{\sin^2\alpha}\small.\)
Ответ: \(\displaystyle \frac{S_{ABCD}}{S_{Y_1Y_2Y_3Y_4}}=\frac{2}{\sin^2\alpha}\small.\)
На рисунке в решении задачи точки \(\displaystyle Y_1,\,Y_2,\,Y_3\) и \(\displaystyle Y_4\) лежат на сторонах параллелограмма. Но если они будут лежать на продолжениях сторон, решение не изменится.