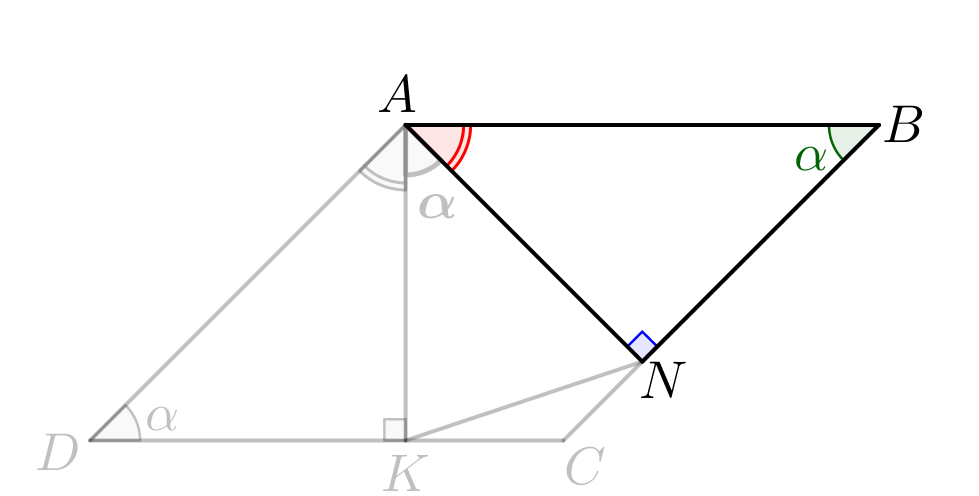
Из вершины тупого угла параллелограмма на две его противоположные стороны опустили высоты. Оказалось, что образованный этими высотами треугольник составляет одну четверть от площади всего параллелограмма. Найдите острый угол параллелограмма.
Из точки \(\displaystyle A\) опустили перпендикуляры \(\displaystyle AK\) и \(\displaystyle AN\small.\) Обозначим острый угол параллелограмма \(\displaystyle CDA\) за \(\displaystyle \alpha\small.\) Противоположные углы параллелограмма равны, значит, \(\displaystyle \angle ABC=\alpha\small.\) То есть необходимо найти \(\displaystyle \alpha\small.\) | 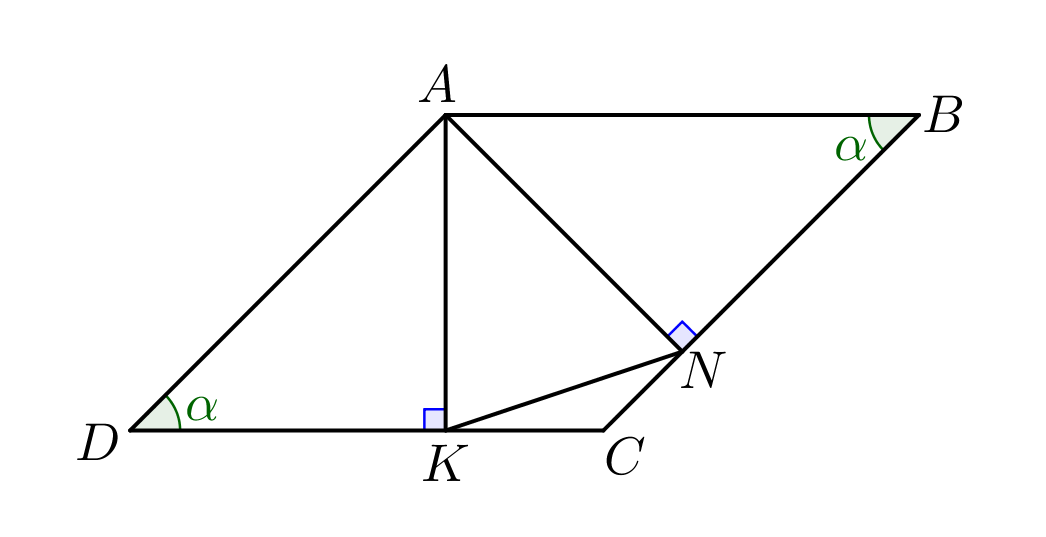 |
Чтобы решить задачу:
- выразим площадь параллелограмма через стороны и \(\displaystyle \alpha\small,\)
- выразим площадь треугольника через те же величины,
- сравним получившиеся формулы.
\(\displaystyle S_{ABCD}=AB\cdot AD\cdot\sin\alpha\small.\)
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними:
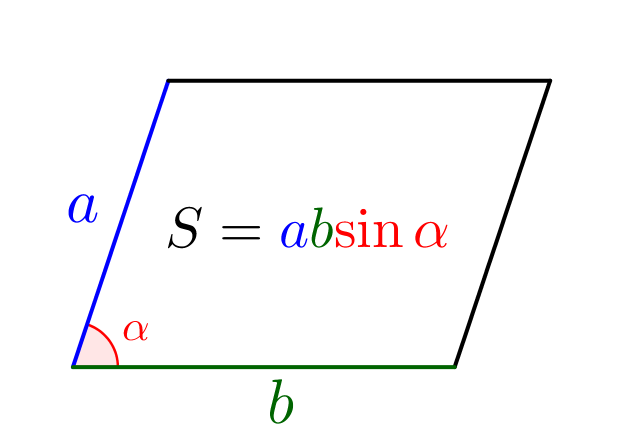
Тогда
\(\displaystyle S_{ABCD}=CD\cdot AD\cdot\sin\alpha\small.\)
Поскольку противоположные стороны параллелограмма равны \(\displaystyle CD=AB\small,\) получаем:
\(\displaystyle S_{ABCD}=AB\cdot AD\cdot\sin\alpha\small.\)
2. Чтобы найти площадь треугольника \(\displaystyle AKN{\small:}\)
- найдем угол \(\displaystyle KAN\small,\)
- выразим \(\displaystyle AK\) и \(\displaystyle AN\) через стороны параллелограмма.
В параллелограмме \(\displaystyle ABCD\) противоположные стороны параллельны: \(\displaystyle AB||CD\small.\) Тогда односторонние углы \(\displaystyle \angle CDA\) и \(\displaystyle \angle DAB\) в сумме дают \(\displaystyle 180^{\circ}\small.\) Значит, \(\displaystyle \angle DAB=180^{\circ}-\alpha\small.\) В треугольниках \(\displaystyle DAK\) и \(\displaystyle BAN\) один из углов \(\displaystyle 90^{\circ}\small,\) а второй угол \(\displaystyle \alpha\small.\) Тогда третий угол: \(\displaystyle \angle DAK=\angle BAN=180^{\circ}-90^{\circ}-\alpha=90^{\circ}-\alpha\small.\) Тогда \(\displaystyle \begin{aligned}\angle KAN=\angle DAB-\angle DAK-\angle BAN=\\=180^{\circ}-\alpha-2\cdot(90^{\circ}-\alpha)=\alpha\small.\end{aligned}\) | 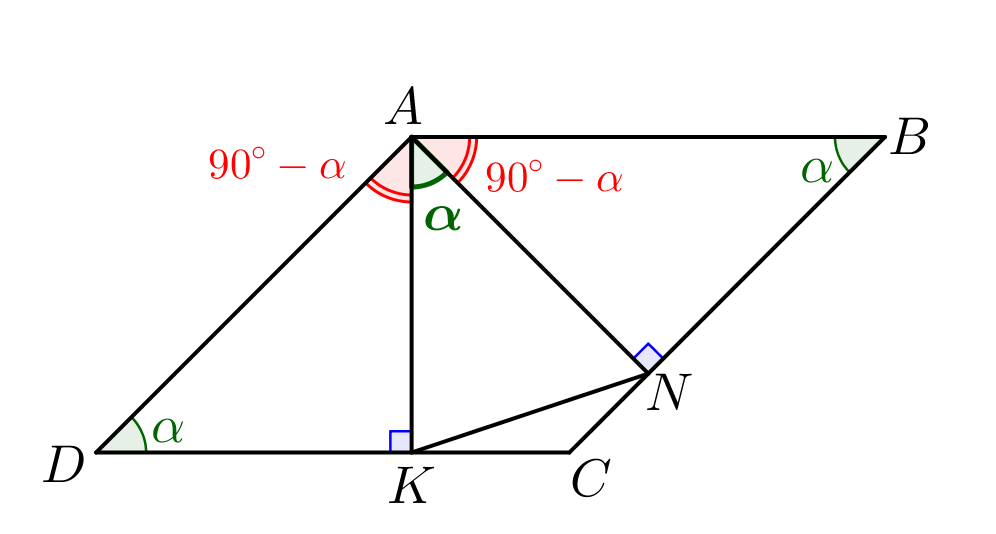 |
\(\displaystyle AK=AD\sin\alpha\small.\)
В прямоугольном треугольнике \(\displaystyle DAK{\small:}\) \(\displaystyle AK=AD\sin\alpha\small.\) | 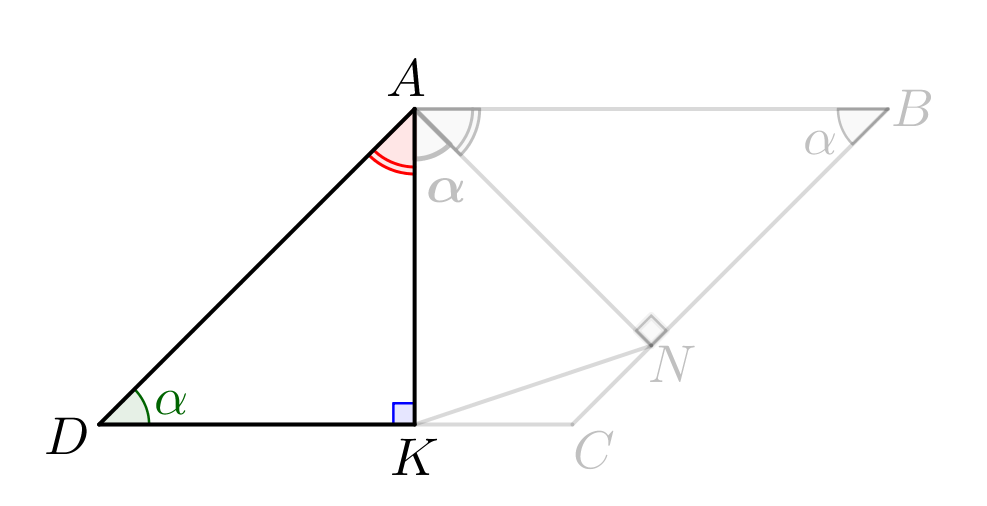 |
\(\displaystyle AN=AB\sin\alpha\small.\)
Тогда площадь треугольника \(\displaystyle KAN{\small:}\)
\(\displaystyle S_{KAN}=\frac{\sin\angle KAN\cdot AK\cdot AN}{2}=\frac{\sin\alpha\cdot(AD\sin\alpha)(AB\sin\alpha)}{2}=\frac{AB\cdot AD\cdot\sin^3\alpha}{2}\small.\)
Отношение площади треугольника к площади параллелограмма равно \(\displaystyle \frac{1}{4}{\small:}\)
\(\displaystyle \frac{1}{4}=\frac{S_{KAN}}{S_{ABCD}}=\frac{\frac{AB\cdot AD\cdot\sin^3\alpha}{2}}{AB\cdot AD\cdot\sin\alpha}=\frac{\sin^2\alpha}{2}\small.\)
Значит,
\(\displaystyle \sin^2\alpha=\frac{1}{2}\small.\)
Синус любого угла от \(\displaystyle 0^{\circ}\) до \(\displaystyle 180^{\circ}\) неотрицательный, тогда
\(\displaystyle \sin\alpha=\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}\small.\)
Острый угол, синус которого \(\displaystyle \frac{\sqrt{2}}{2}\small,\) равен \(\displaystyle 45^{\circ}\small.\) То есть
\(\displaystyle \alpha=45^{\circ}\small.\)
Ответ: \(\displaystyle \alpha=45^{\circ}\small.\)