В треугольнике \(\displaystyle ABC\) на стороне \(\displaystyle AB\) взяты точки \(\displaystyle D{\small ,\;}E{\small ,\;}F{\small .}\)
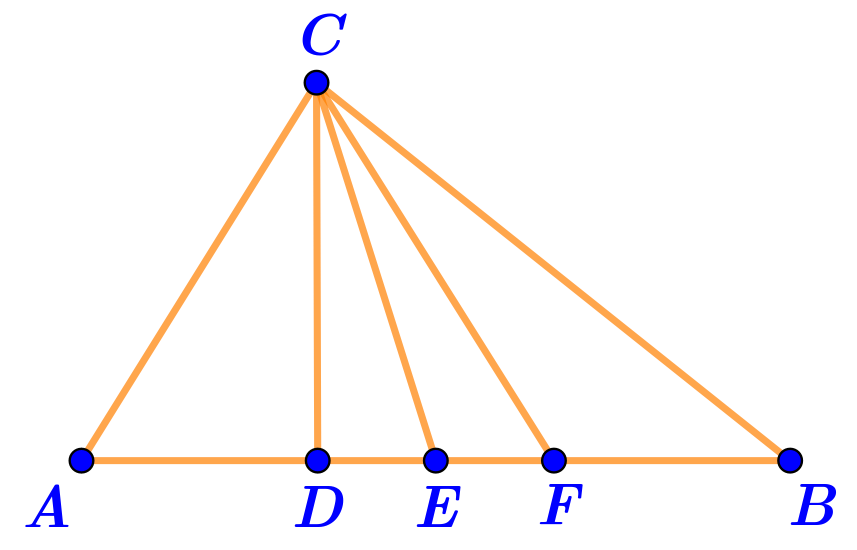
Известно, что \(\displaystyle AF=CF{\small ,\;}AE=BE{\small ,\;}\angle ADC=90\degree {\small .}\)
Какой отрезок является медианой треугольника \(\displaystyle ABC{\normalsize\; ?}\)
Медиана треугольника
Медианой треугольника называется отрезок, соединяющий его вершину с серединой противолежащей стороны.
На рисунке отрезок \(\displaystyle BM\)– медиана треугольника \(\displaystyle ABC{\small .}\)
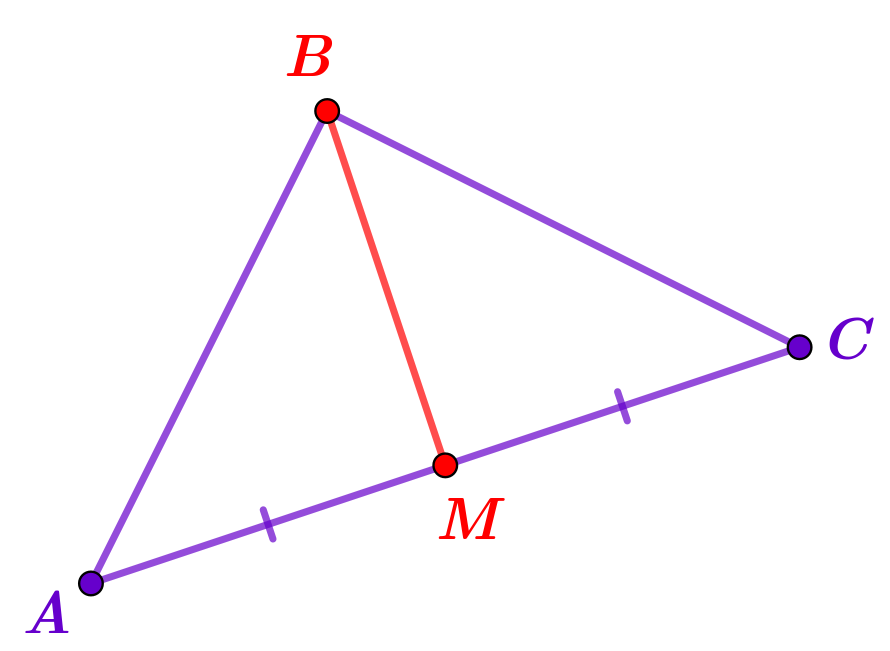
1. Из рисунка следует, что медиана в треугольнике \(\displaystyle ABC\) может быть построена из точки \(\displaystyle C{\small .}\)
Определим, какая из точек \(\displaystyle D{\small ,}\)\(\displaystyle E{\small ,}\)\(\displaystyle F\) является серединой отрезка \(\displaystyle AB{\small .}\)
2. В условиях задачи найдём равенство длин отрезков:
\(\displaystyle AE=BE\).
Значит, точка \(\displaystyle E\,-\) середина стороны \(\displaystyle AB{\small .}\)
То есть отрезок \(\displaystyle EC\) является медианой треугольника \(\displaystyle ABC\) по определению.
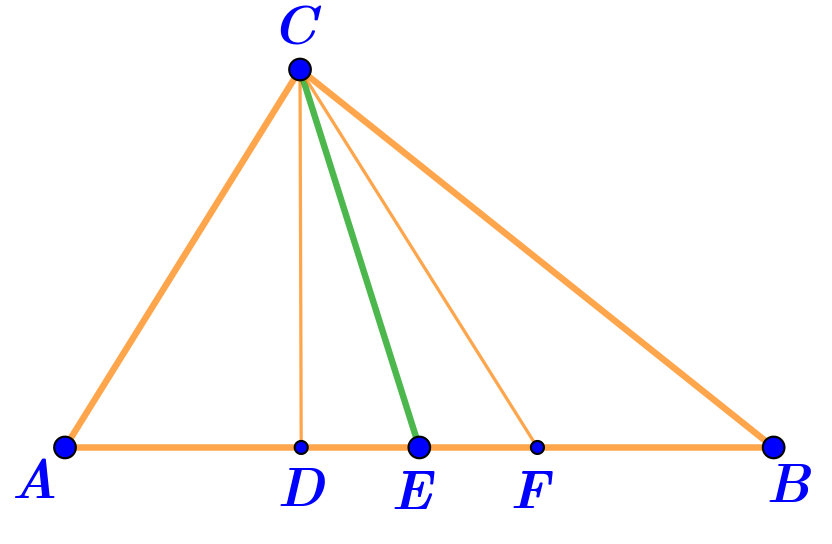
Ответ: медианой треугольника \(\displaystyle ABC\) является отрезок отрезок \(\displaystyle EC{\small .}\)