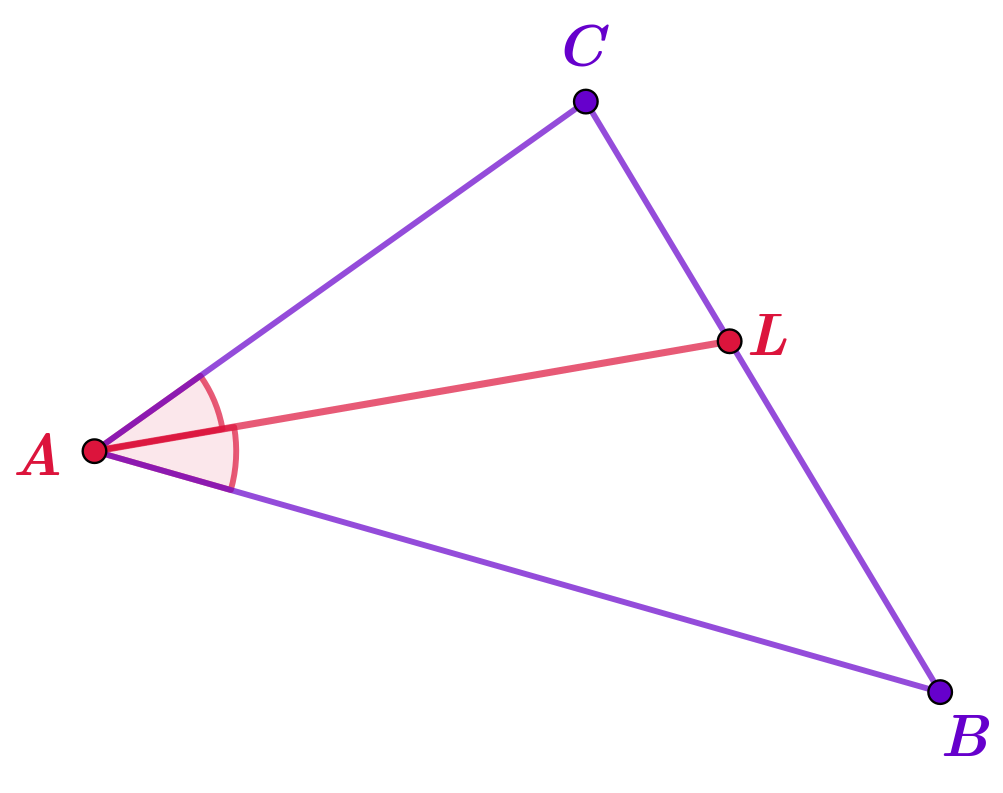
Два треугольника \(\displaystyle ABP\) и \(\displaystyle ABQ\) имеют общую сторону \(\displaystyle AB{\small .}\)
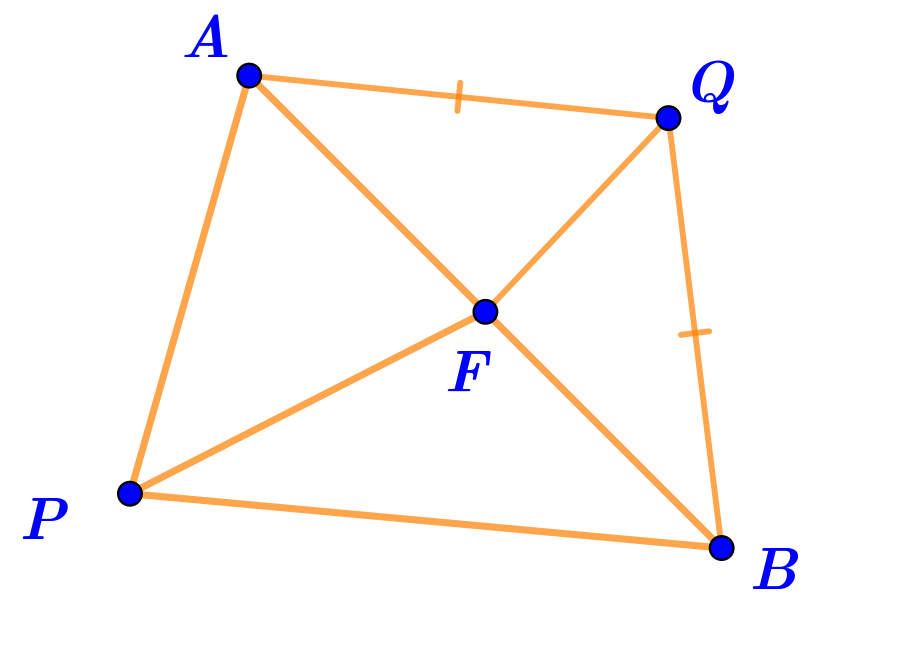
В треугольнике \(\displaystyle ABQ\) провели биссектрису \(\displaystyle QF{\small .}\) При этом точка \(\displaystyle F\) не попала на прямую \(\displaystyle PQ{\small .}\)
Известно, что \(\displaystyle AQ=BQ\).
Какую роль играет отрезок \(\displaystyle PF\) в треугольнике \(\displaystyle ABP\,?\)
Отрезок \(\displaystyle PF -\) треугольника \(\displaystyle ABP{\small .}\)
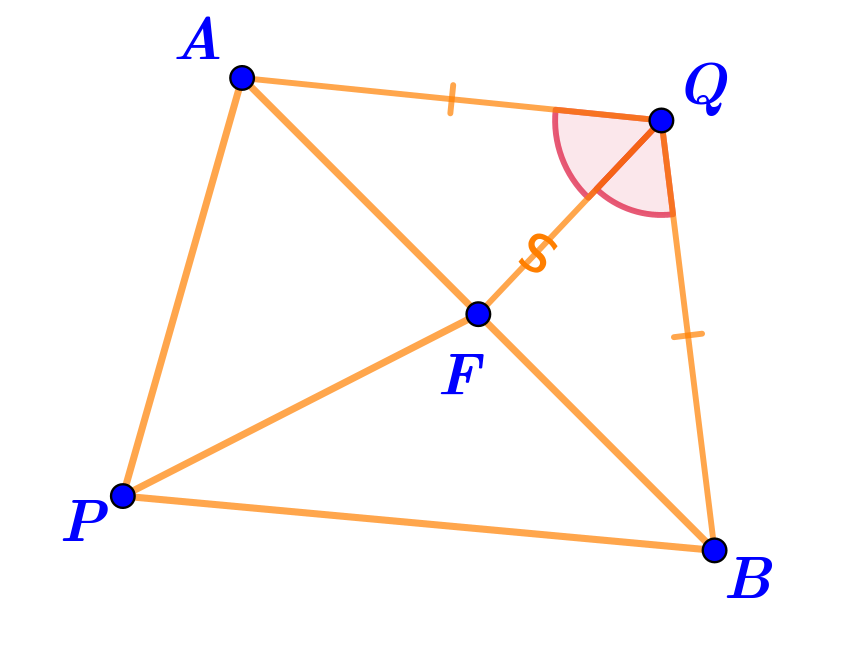
Треугольники \(\displaystyle AQF\) и \(\displaystyle BQF\) равны по первому признаку:
\(\displaystyle \left\{\begin{array}{ll}AQ=QB\\QF - \text{ \footnotesize\it общая сторона}\\\angle AQF=\angle BQF\end{array}{\LARGE\Rightarrow}\quad\begin{array}{c} \\{\bf\triangle}AQF={\bf\triangle}BQF\\\text{ \footnotesize\it(по первому признаку)}\end{array}\right.\)
В равных треугольниках равны стороны, расположенные напротив равных углов:
\(\displaystyle AF=BF{\small .}\)
Значит, точка \(\displaystyle F\)– середина стороны \(\displaystyle AB{\small .}\)
Отрезок \(\displaystyle PF\)– медиана треугольника \(\displaystyle ABP\) по определению.
Ответ: медиана.