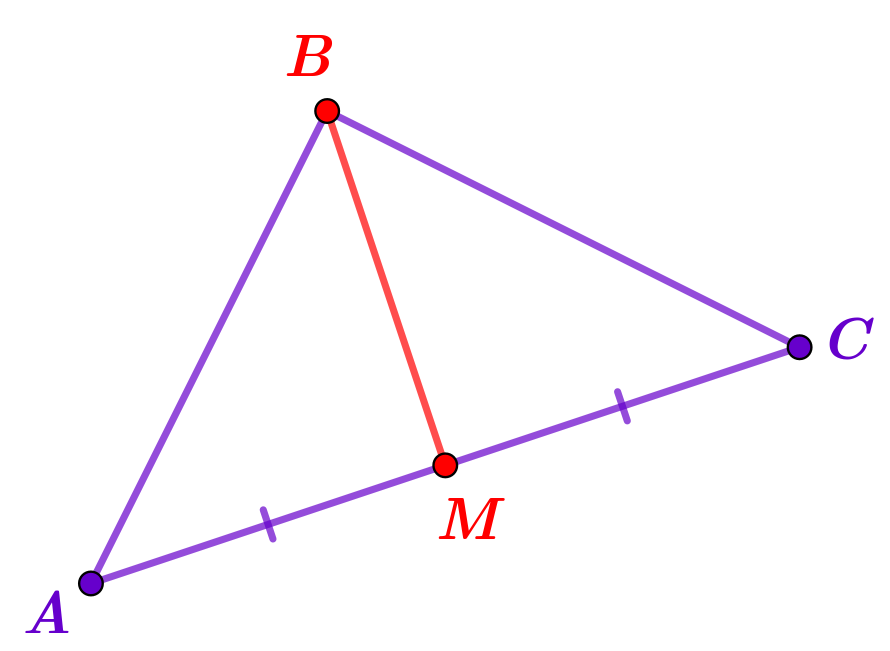
В треугольнике \(\displaystyle ABC\) известно, что \(\displaystyle AB=10\,{\footnotesize см}{\small ,\;}BC=13\,{\footnotesize см}{\small ,\;}AC=16\,{\footnotesize см}{\small .}\)
Из вершины \(\displaystyle B\) проведена медиана \(\displaystyle BM{\small .}\)
Какова длина отрезка \(\displaystyle AM\,?\) Ответ дайте в сантиметрах.
\(\displaystyle AM=\)\(\displaystyle {\footnotesize см}\)
Сделаем рисунок.
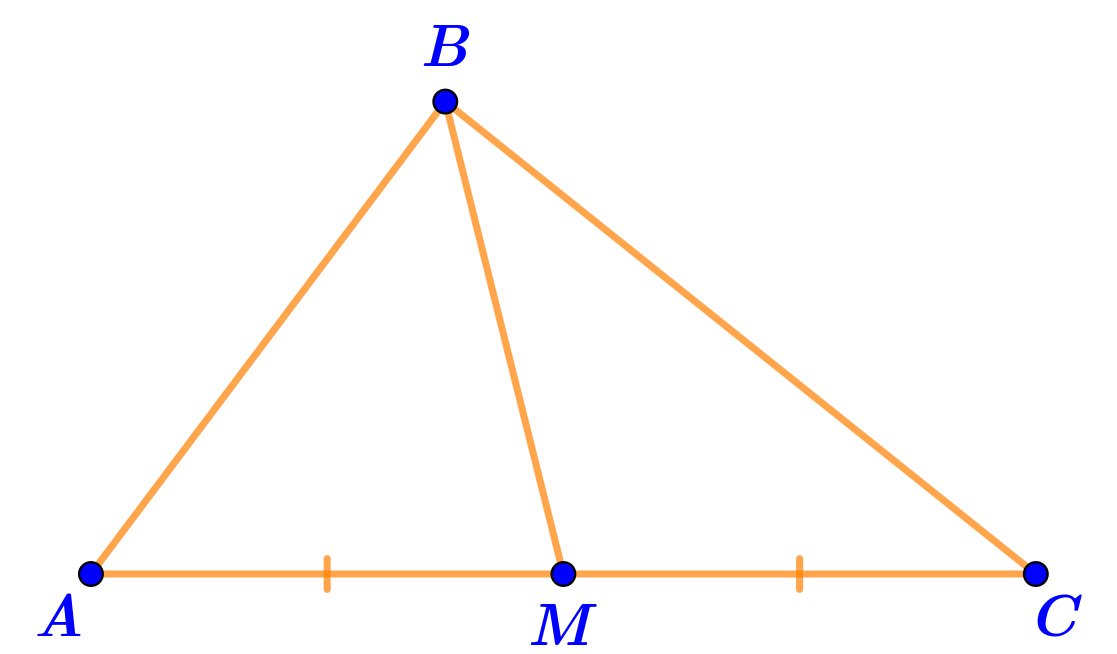
Значит, длина отрезка \(\displaystyle AM\) составляет половину длины стороны \(\displaystyle AC{\small :}\)
\(\displaystyle AM=\frac{AC}{2}{\small .}\)
В данной задаче
\(\displaystyle AC=16\,{\footnotesize см.}\)
Тогда
\(\displaystyle AM=\frac{16}{2}=\)\(\displaystyle 8\,({\footnotesize см}){\small .}\)
Ответ: \(\displaystyle 8\,{\footnotesize см}{\small .}\)