В треугольнике \(\displaystyle ABC\) проведены медианы \(\displaystyle AN\) и \(\displaystyle BM{\small .}\)
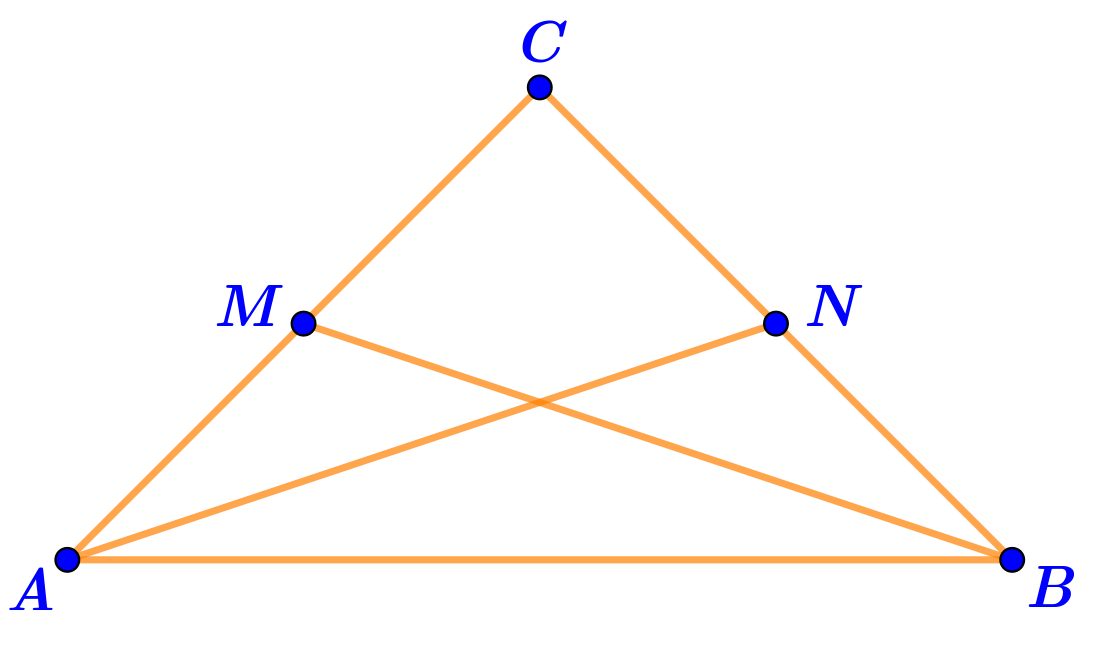
В треугольнике \(\displaystyle BMC\) известны \(\displaystyle BM=11\,{\footnotesize см}{\small ,}\;MC=5\,{\footnotesize см}{\small ,\;}BC=10\,{\footnotesize см}{\small .}\)
Найти длину медианы \(\displaystyle AN{\small .}\) Ответ дайте в сантиметрах.
\(\displaystyle AN=\) \(\displaystyle {\footnotesize см}\)
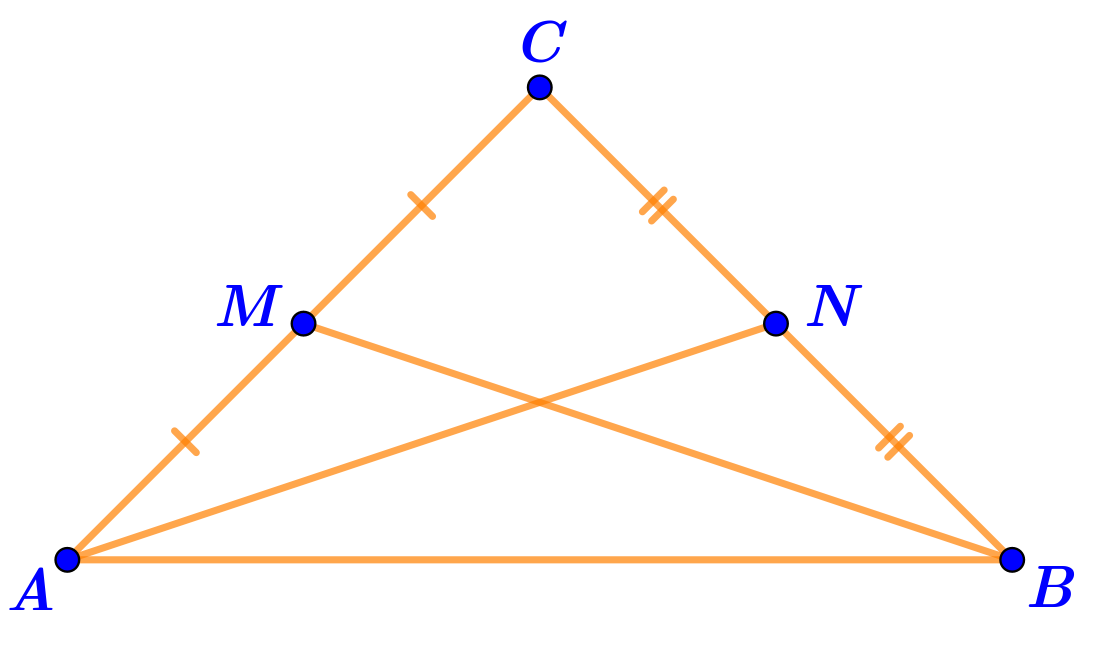
Точка \(\displaystyle N\,-\) середина стороны \(\displaystyle CB{\small .}\)
Значит длина отрезка \(\displaystyle CN\) равна половине длины отрезка \(\displaystyle CB{\small :}\)
\(\displaystyle CN=\frac{CB}{2}=5\,{\footnotesize см}{\small .}\)
В данной задаче
\(\displaystyle CM=5\,{\footnotesize см}{\small .}\)
Тогда
\(\displaystyle CN=CM=MA{\small .}\)
Уточним обозначения равных элементов на рисунке.
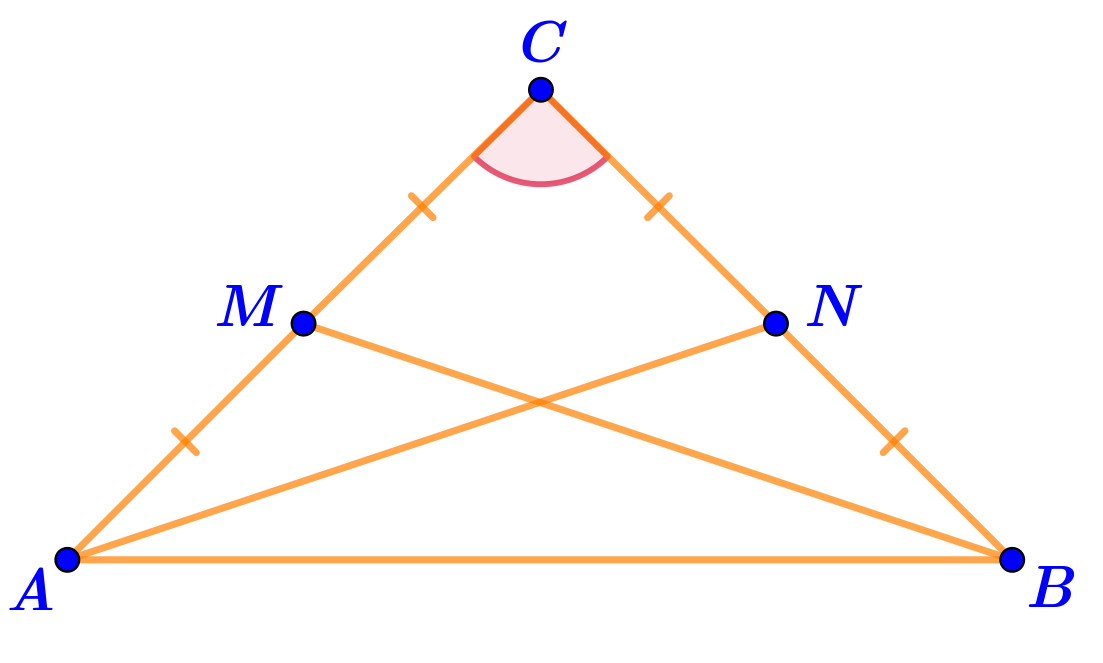
В равных треугольниках напротив общего угла лежат равные стороны:
\(\displaystyle AN=BM=\)\(\displaystyle \color{green}{11\,{\footnotesize см}}{\small .}\)
Ответ: \(\displaystyle 11\,{\footnotesize см}{\small .}\)