Докажем геометрическим способом формулу:
Для любых положительных чисел \(\displaystyle a,\, b\) верно следующее тождество:
\(\displaystyle (a+b\,)(a-b\,)=a^{\,2}-b^{\, 2}.\)
Для определенности будем считать, что \(\displaystyle a>b.\)
Произведение \(\displaystyle (a-b\,)(a+b\,)\) является площадью прямоугольника со сторонами \(\displaystyle (a-b\,)\) и \(\displaystyle (a+b\,).\) Построим данный прямоугольник:
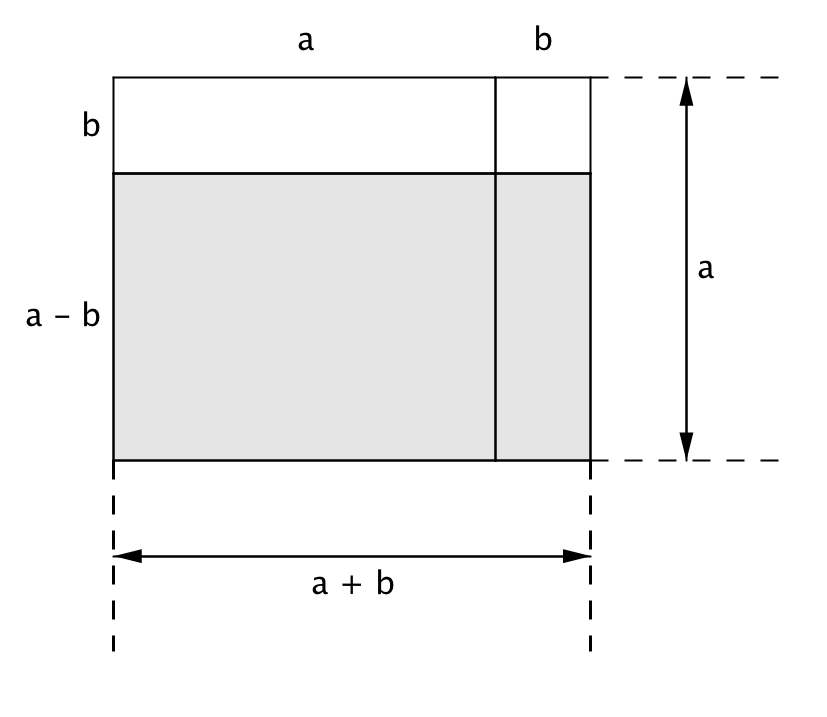
Площадь этого прямоугольника (закрашенного серым цветом) равна произведению длин его сторон, то есть \(\displaystyle (a-b\,)(a+b\,):\)
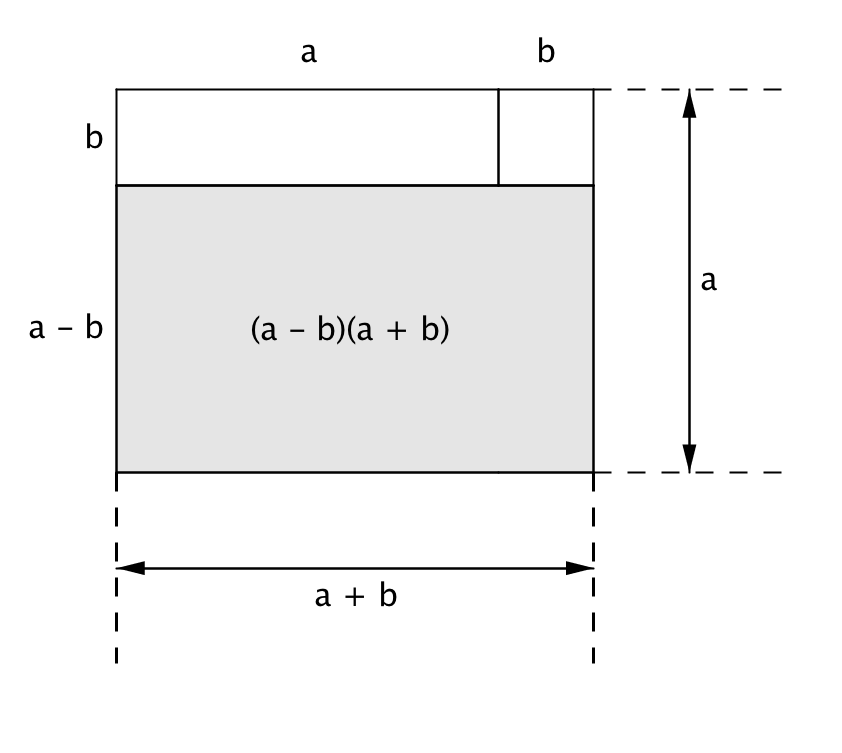
Вычислим площадь этого прямоугольника другим способом.
Эта площадь равна сумме площадей двух прямоугольников: площади прямоугольника "1" со сторонами \(\displaystyle (a-b\,)\) и \(\displaystyle a\)

и площади прямоугольника "2" со сторонами \(\displaystyle (a-b\,)\) и \(\displaystyle b\)
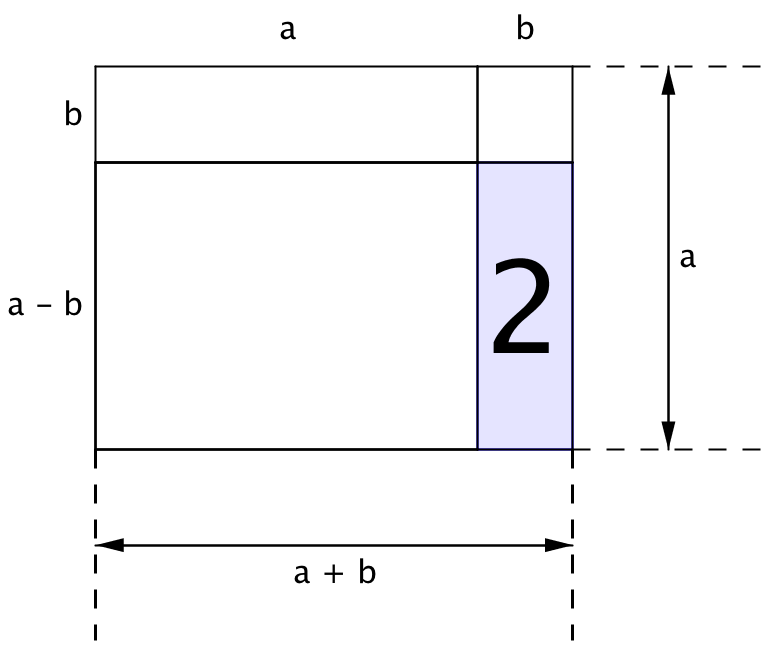

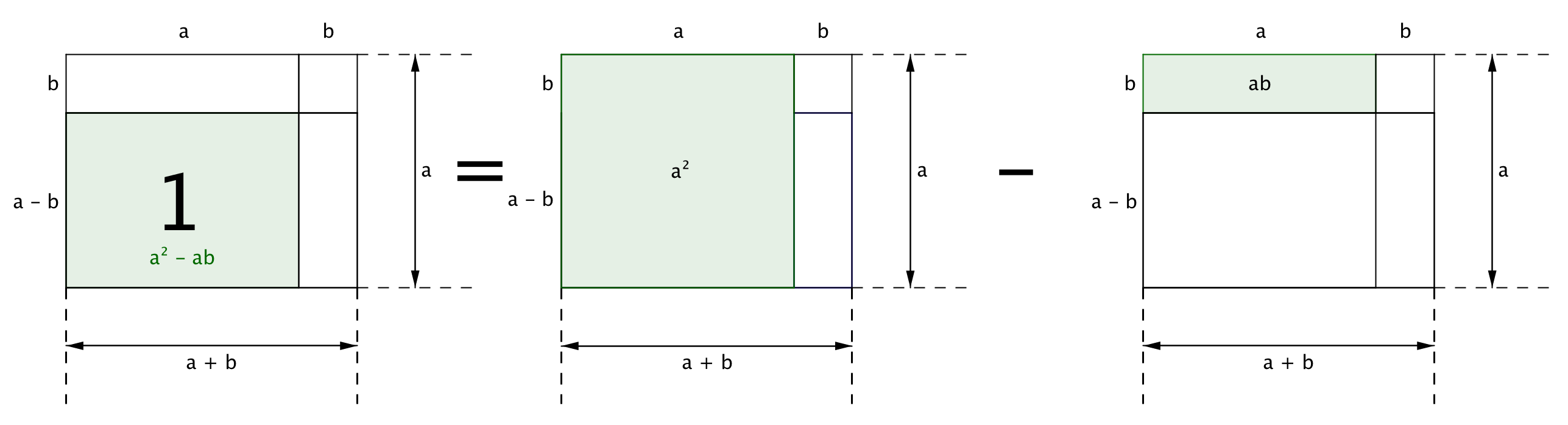
Найдем площадь каждого из прямоугольников и сложим их. В результате получим площадь данного прямоугольника.
Площадь прямоугольника "1" равна разности площадей квадрата со стороной \(\displaystyle a\) и прямоугольника со сторонами \(\displaystyle a\) и \(\displaystyle b:\)
\(\displaystyle a^{\,2}-ab\)
Площадь прямоугольника "2" равна разности площадей прямоугольника со сторонами \(\displaystyle a\) и \(\displaystyle b\) и квадрата со стороной \(\displaystyle b:\)
\(\displaystyle ab-b^{\,2}\)
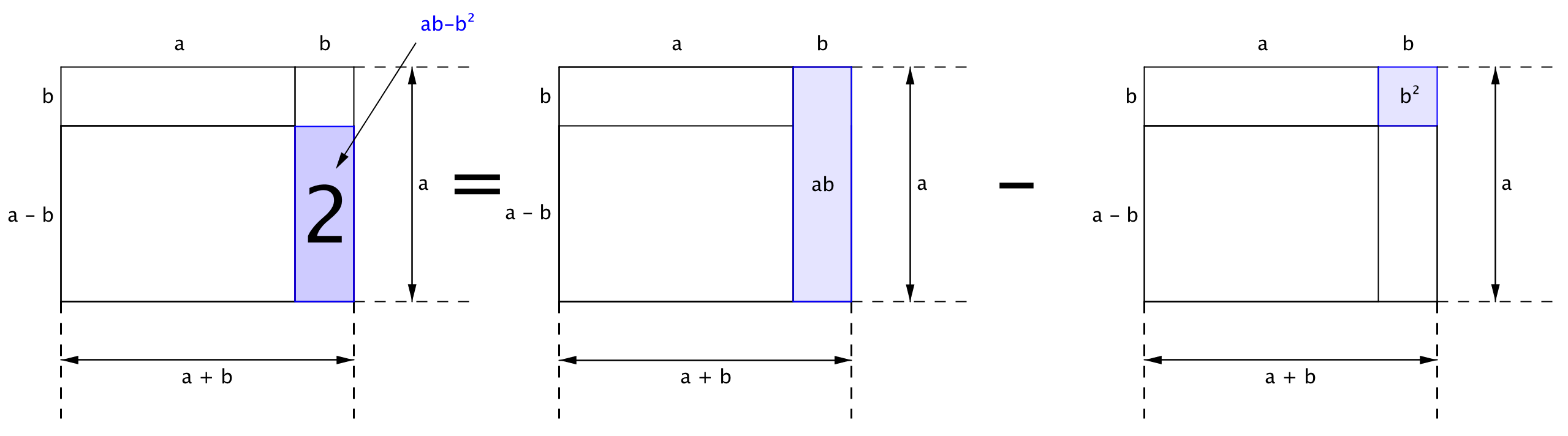
Таким образом, площадь прямоугольника со сторонами \(\displaystyle (a-b\,)\) и \(\displaystyle (a+b\,)\) равна сумме площадей прямоугольников "1" и"2":
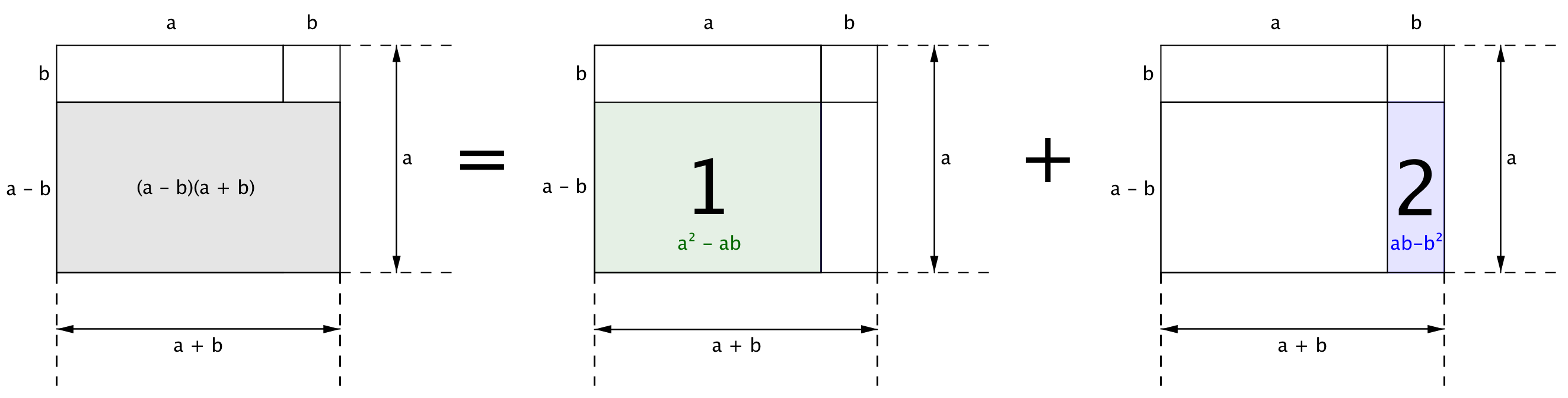
\(\displaystyle (a-b\,)(a+b\,)=(a^2-ab\,)+(ab-b^2\,).\)
Раскроем скобки:
\(\displaystyle (a-b\,)(a+b\,)=(a^{\,2}-ab\,)+(ab-b^{\,2}\,)=a^{\,2}-ab+ab-b^{\,2}=a^{\,2}-b^{\,2}.\)
Таким образом, мы доказали формулу "разность квадратов" геометрическим способом.