Skip to main content

Теория: 15 Практическое применение теорем синусов и косинусов

Задание

 Два парохода начинают свое движение из одного и того же пункта и двигаются равномерно по прямым, пересекающимся под углом \(\displaystyle 60^\circ\small.\) Скорость первого парохода \(\displaystyle 65\) км/ч, а второго – \(\displaystyle 75\) км/ч. Вычислите, на каком расстоянии друг от друга будут пароходы через \(\displaystyle 4\) часа. Ответ дайте в км.

\(\displaystyle S=\)
20\sqrt{199}
км
Решение

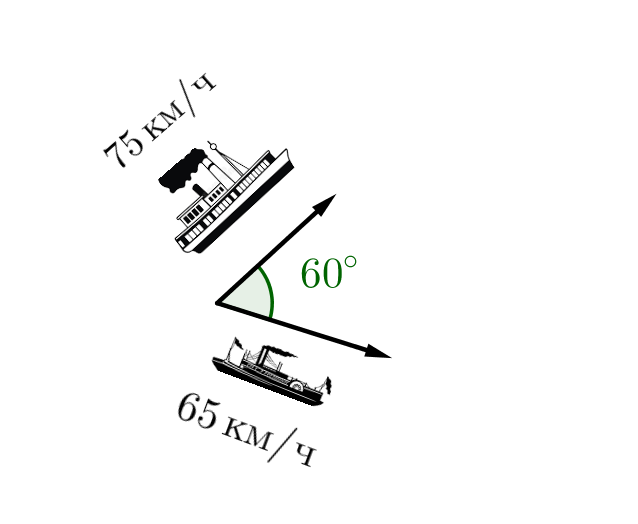
За \(\displaystyle 4\) часа движения теплоходы пройдут:

\(\displaystyle 75\cdot4=300\)км и \(\displaystyle 65\cdot4=260\)км.

Построим рисунок к задаче:

 

  • \(\displaystyle AB=300\small,\)
  • \(\displaystyle AC=260\small,\)
  • \(\displaystyle \angle BAC=60º \small.\)

Через \(\displaystyle 4\) часа расстояние между теплоходами будет равно \(\displaystyle BC\small.\)

 

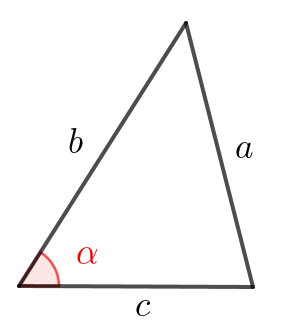
Запишем теорему косинусов для треугольника \(\displaystyle ABC\small.\)

\(\displaystyle BC^2=AB^2+AC^2-2\cdot AB\cdot AC\cdot \cos\angle BAC\small.\)


Подставим в формулу известные значения \(\displaystyle AB=300,\,AC=260\) и \(\displaystyle \angle BAC=60^\circ{\small:}\)

\(\displaystyle BC^2=300^2+260^2-2\cdot 300\cdot 260\cdot \frac{1}{2}=90000+67600-78000=79600\small,\)

\(\displaystyle BC=\sqrt{79600}=20\sqrt{199}\small.\)

Ответ: \(\displaystyle 20\sqrt{199}\)км.