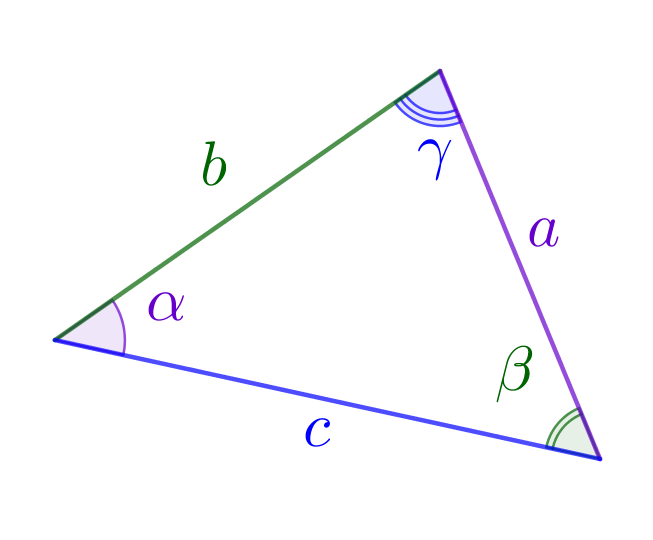
Вершина горы из точки \(\displaystyle A\) видна под углом \(\displaystyle 30^\circ\small,\) а при приближении к горе на \(\displaystyle 200\)м вершина стала видна под углом \(\displaystyle 40^\circ\small.\) Найдите высоту горы в метрах. Ответ округлите до целых.
Чтобы найти приближенные значения синуса и косинуса, введите значение угла в градусах и нажмите "enter":
Обозначим искомый отрезок \(\displaystyle CH\) за \(\displaystyle x\small.\) | 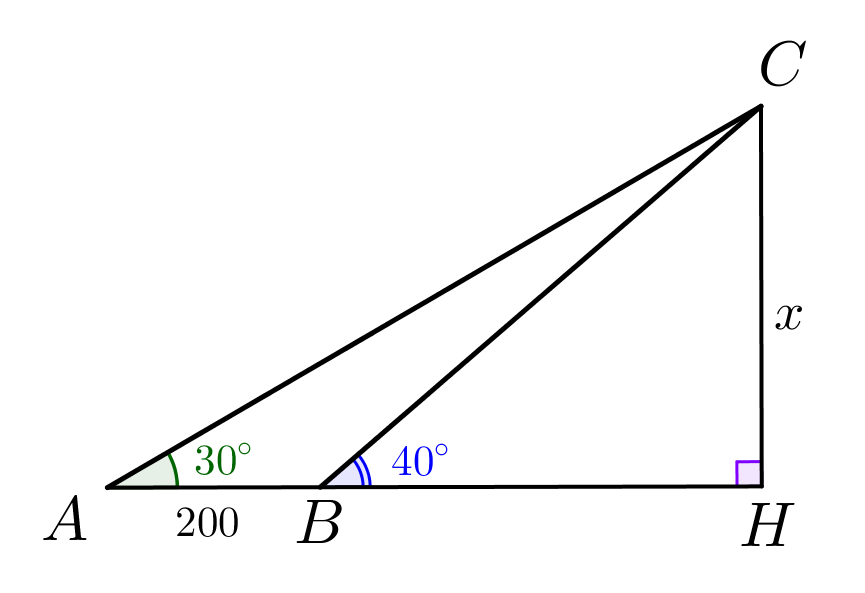 |
Из прямоугольного треугольника \(\displaystyle BCH\) выразим \(\displaystyle x\small,\) используя известный угол:
\(\displaystyle x=BC\cdot \sin40^\circ\small.\)
Расмотрим треугольник \(\displaystyle ABC\) и выразим \(\displaystyle BC\small.\)
Найдем градусные меры углов треугольника \(\displaystyle ABC\small.\) Угол \(\displaystyle ABC\) является смежным для угла \(\displaystyle CBH\) и равен: \(\displaystyle \angle ABC=180^\circ-\angle CBH=180^\circ-40^\circ=140^\circ\small.\) Тогда угол \(\displaystyle ACB\) равен: \(\displaystyle \begin{aligned}\angle ACB&=180^\circ-\angle CAB-\angle ABC= \\ &=180^\circ-30^\circ-140^\circ=10^\circ\small.\end{aligned}\) | 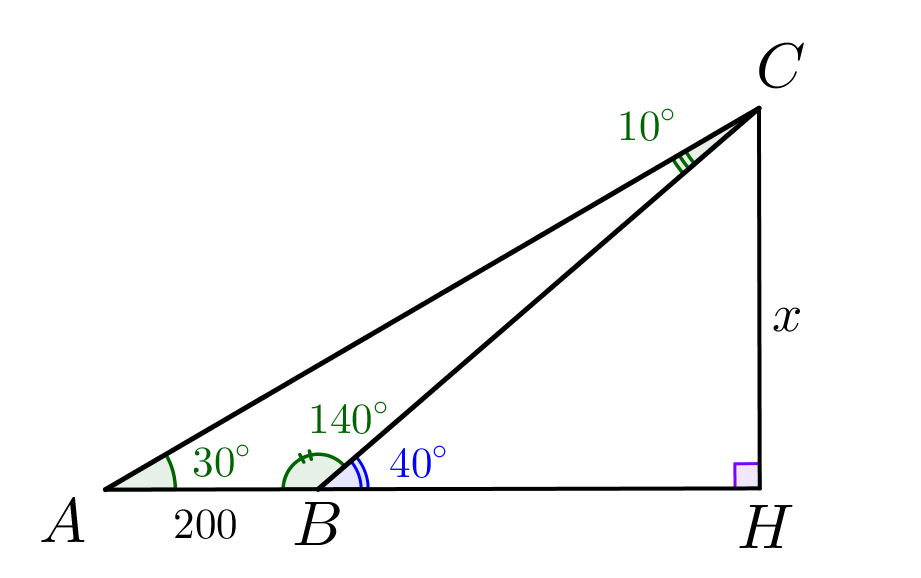 |
\(\displaystyle \frac{BC}{\sin30^\circ}=\frac{AB}{\sin10^\circ}\small.\)
Выразим \(\displaystyle BC\small{:}\)
\(\displaystyle BC=\frac{AB\cdot \sin30^\circ}{\sin10^\circ}\small.\)
Подставим полученное значение в выражение для \(\displaystyle x\small{:}\)
\(\displaystyle x=\frac{AB\cdot \sin30^\circ}{\sin10^\circ}\cdot \sin40^\circ \approx \frac{200\cdot \frac{1}{2}\cdot 0{,}643}{0{,}174}\approx 369{,}54\approx370\small.\)
Ответ: \(\displaystyle 370\)м.