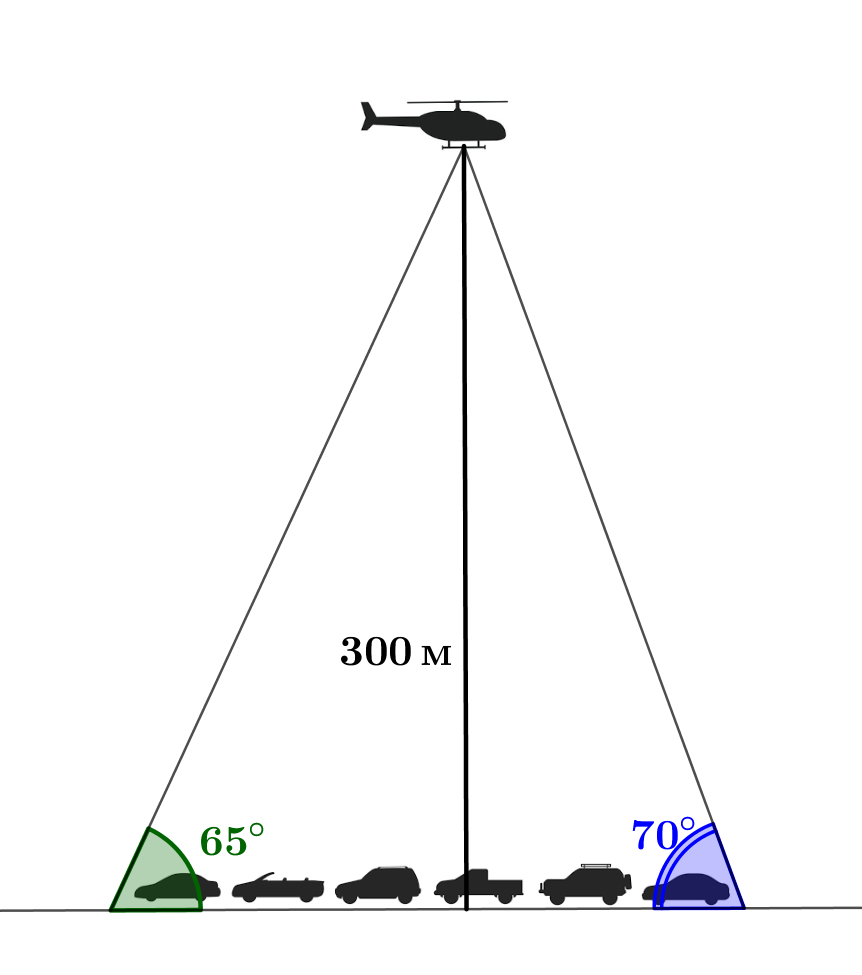
С вертолета, находящегося над шоссейной дорогой, была замечена двигавшаяся по ней колонна машин. Начало колонны видно под углом понижения \(\displaystyle 65^\circ\small,\) а конец – под углом \(\displaystyle 70^\circ\small.\) Найдите длину колонны в метрах, если вертолет находится на высоте \(\displaystyle 300\) м. Ответ округлите до целых.
Чтобы найти приближенные значения синуса и косинуса, введите значение угла в градусах и нажмите "enter":
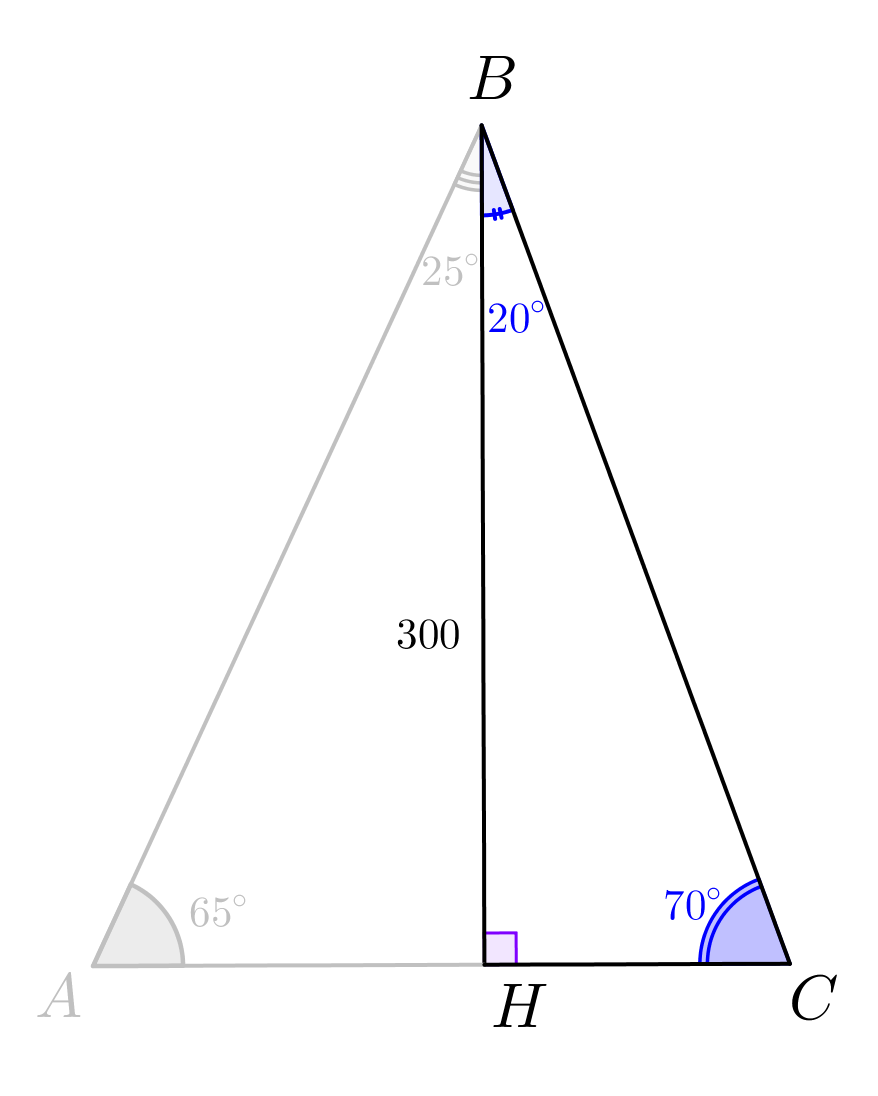
\(\displaystyle AC\) — длина колонны. | 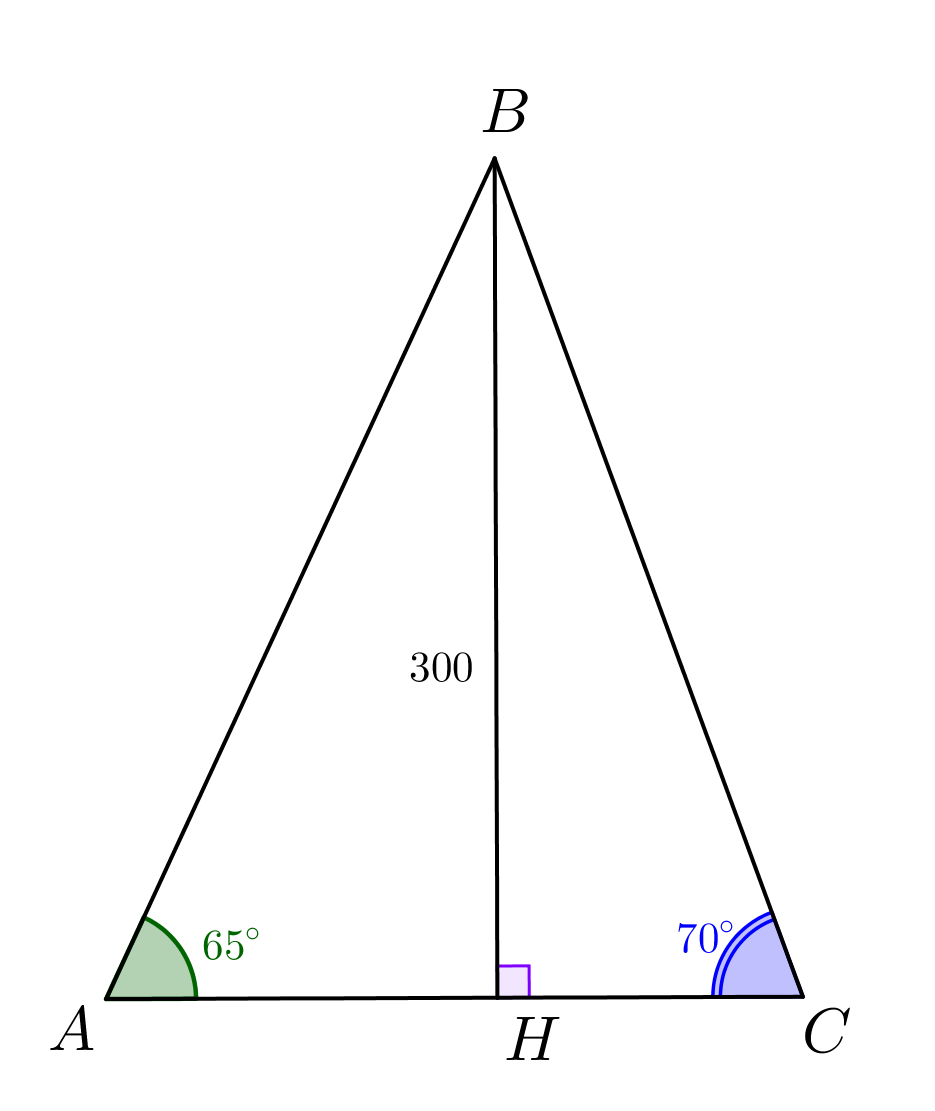 |
Отрезок \(\displaystyle AC\) состоит из отрезков \(\displaystyle AH\) и \(\displaystyle HC\small{:}\)
\(\displaystyle AC=AH+HC\small.\)
\(\displaystyle AH=\frac{BH\cdot\sin25^\circ}{\sin65^\circ}\small.\)
Рассмотрим треугольник \(\displaystyle ABH\small{:}\) \(\displaystyle \begin{aligned}\angle ABH&=180^\circ-\angle BHA-\angle BAH= \\ &=180^\circ-90^\circ-65^\circ=25^\circ\small.\end{aligned}\) По теореме синусов: \(\displaystyle \frac{AH}{\sin25^\circ}=\frac{BH}{\sin65^\circ}\small.\) Выразим \(\displaystyle AH\small{:}\) \(\displaystyle AH=\frac{BH\cdot \sin25^\circ}{\sin65^\circ}\small.\) | 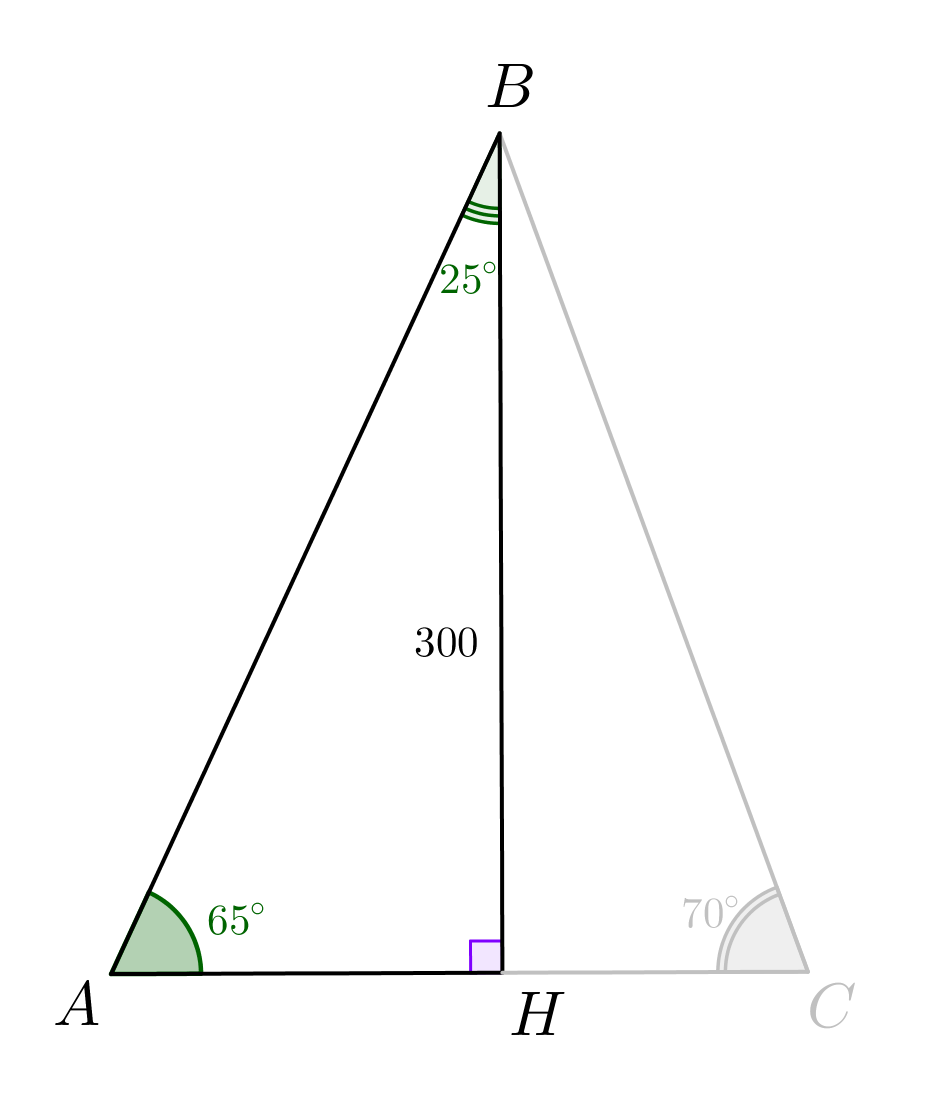 |
\(\displaystyle HC=\frac{BH\cdot\sin20^\circ}{\sin70^\circ}\small.\)
Тогда
\(\displaystyle AC=AH+HC=\frac{BH\cdot\sin25^\circ}{\sin65^\circ}+\frac{BH\cdot\sin20^\circ}{\sin70^\circ}=BH\cdot \left(\frac{\sin25^\circ}{\sin65^\circ}+\frac{\sin20^\circ}{\sin70^\circ}\right)\small.\)
Подставим известные значения и вычислим длину \(\displaystyle AC\small{:}\)
\(\displaystyle AC=300\cdot \left(\frac{0{,}423}{0{,}906}+\frac{0{,}342}{0{,}94}\right)\approx 249{,}215\approx 249\small.\)
Данную задачу можно решить, не используя теорему синусов.
Из треугольника \(\displaystyle ABH\) получаем, что:
\(\displaystyle AH=\frac{BH}{\tg 65^\circ}\small.\)
А из треугольника \(\displaystyle BCH\) получаем, что:
\(\displaystyle CH=\frac{BH}{\tg 70^\circ}\small.\)
Тогда
\(\displaystyle AC=AH+HC=\frac{BH}{\tg 65^\circ}+\frac{BH}{\tg 70^\circ}=\frac{300}{2{,}14}+\frac{300}{2{,}75}\approx 249{,}28\approx 249\small.\)
Ответ: \(\displaystyle 249\)м.