Велосипедист едет по замкнутому треугольному маршруту. Два угла этого треугольника равны \(\displaystyle 70^\circ\) и \(\displaystyle 80^\circ\small.\) Меньшую сторону он проехал за \(\displaystyle 1\)ч. За сколько часов он проедет весь маршрут, сохраняя постоянную скорость? Ответ округлите до десятых.
Чтобы найти приближенные значения синуса и косинуса, введите значение угла в градусах и нажмите "enter":
Напротив меньшего угла в треугольнике лежит меньшая сторона, поэтому меньшая сторона в треугольнике \(\displaystyle ABC\) – это \(\displaystyle AC\small.\) | 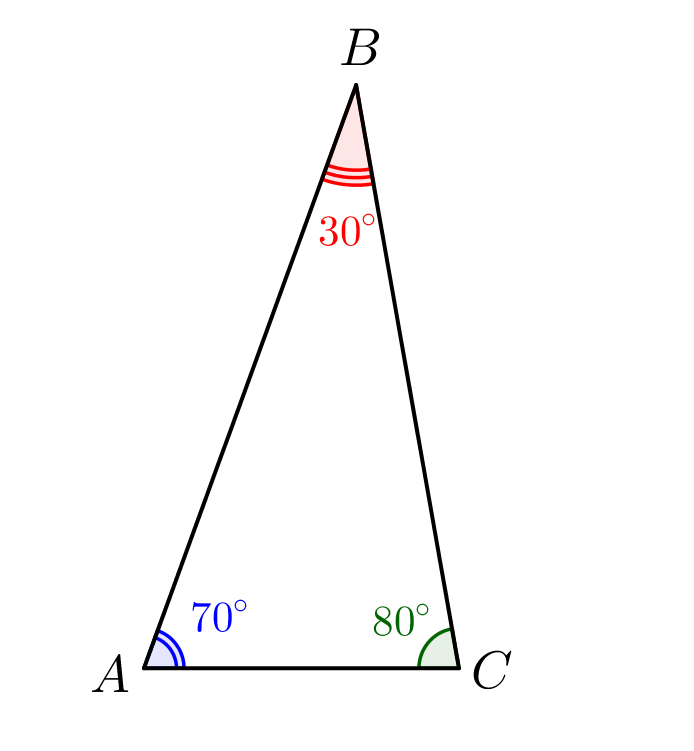 |
\(\displaystyle \frac{AB}{\sin 80^\circ}=\frac{BC}{\sin 70^\circ}=\frac{AC}{\sin 30^\circ}\small.\)
Время на преодоление стороны \(\displaystyle AC\) известно. Тогда выразим две других стороны маршрута через \(\displaystyle AC\small{:}\)
\(\displaystyle AB=\frac{AC\cdot \sin 80^\circ}{\sin 30^\circ}\small,\)
\(\displaystyle BC=\frac{AC\cdot \sin 70^\circ}{\sin 30^\circ}\small.\)
\(\displaystyle t=t_{AB}+t_{BC}+t_{AC}=\frac{\sin 80^\circ}{\sin 30^\circ}+\frac{\sin 70^\circ}{\sin 30^\circ}+1\approx 4{,}8\small.\)
Ответ: \(\displaystyle 4{,}8\)ч.