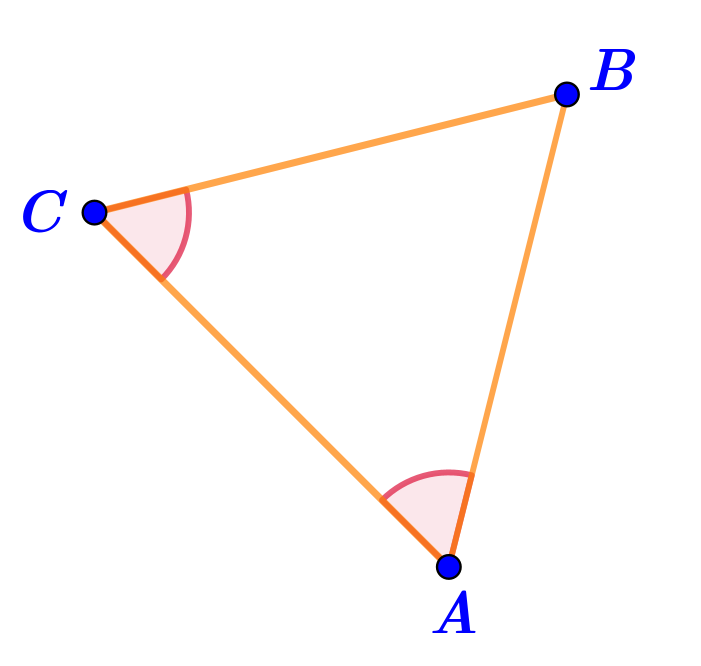
В треугольнике \(\displaystyle ABC\) отмечены два равных угла.
Известны длины двух сторон: \(\displaystyle AC=101\)\(\displaystyle {\footnotesize мм}\), \(\displaystyle AB=102\)\(\displaystyle {\footnotesize мм}{\small.}\)
Каков периметр этого треугольника в миллиметрах?
\(\displaystyle P_{ABC}=\)мм
Отмечена пара равных углов треугольника:
\(\displaystyle \angle BCA = \angle BAC{\small .}\)
Если в треугольнике два угла равны, то он равнобедренный.
Сторона, к которой прилежат равные углы — основание треугольника, две другие — его боковые стороны.
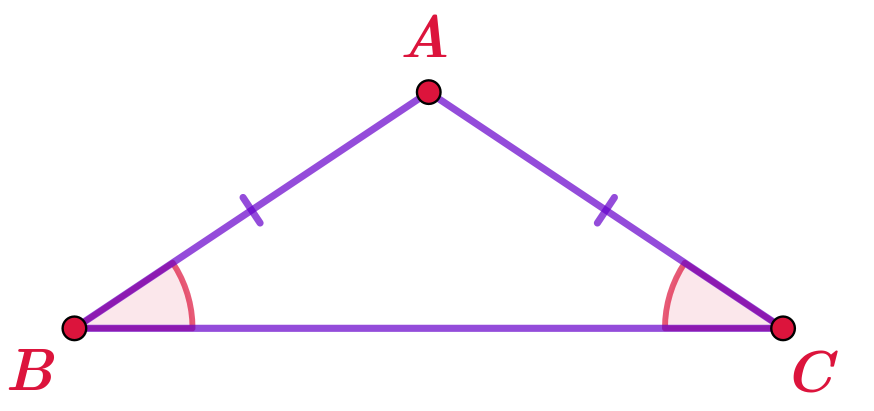
На рисунке \(\displaystyle \angle ABC=\angle ACB{\small .}\)
Сторона \(\displaystyle BC\) — основание треугольника, \(\displaystyle AB\) и \(\displaystyle AC\) — боковые стороны.
Получили:
- углы \(\displaystyle BCA \) и \(\displaystyle BAC\) — углы при основании;
- отрезок \(\displaystyle AC\)— основание треугольника \(\displaystyle ABC{\small ;}\)
- отрезки \(\displaystyle BC=BA\) — боковые стороны равнобедренного треугольника.
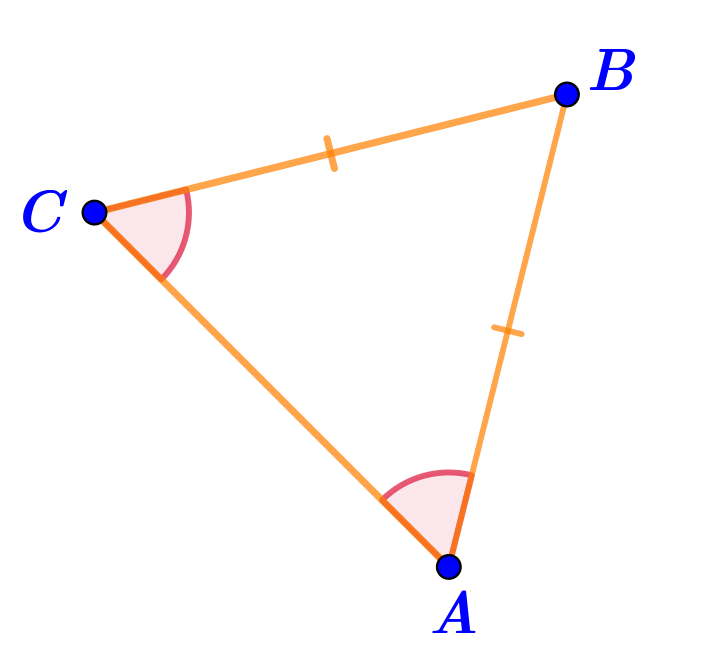
Учитывая равенство \(\displaystyle BC=BA{\small ,}\) все длины сторон треугольника нам известны и выражены в одинаковых единицах:
\(\displaystyle AC=101\, {\footnotesize мм}\) и \(\displaystyle BC=AB=102\, {\footnotesize мм}{\small.}\)
Тогда периметр \(\displaystyle P\) треугольника \(\displaystyle ABC\) равен
\(\displaystyle P=AB+BC+AC=102+102+101=305\, {\footnotesize мм}{\small.}\)
Ответ: \(\displaystyle 305\, {\footnotesize мм}{\small.}\)