Точки \(\displaystyle K{\small ,\;}L\) и \(\displaystyle M\) принадлежат одной прямой, а точка \(\displaystyle N\) не принадлежит ей.
Известны величины углов: \(\displaystyle \angle LKN=57\degree \) и \(\displaystyle \angle MLN=123\degree {\small .}\)
Длина отрезка \(\displaystyle LN\) составляет \(\displaystyle 12\,{\footnotesize см}{\small .}\)
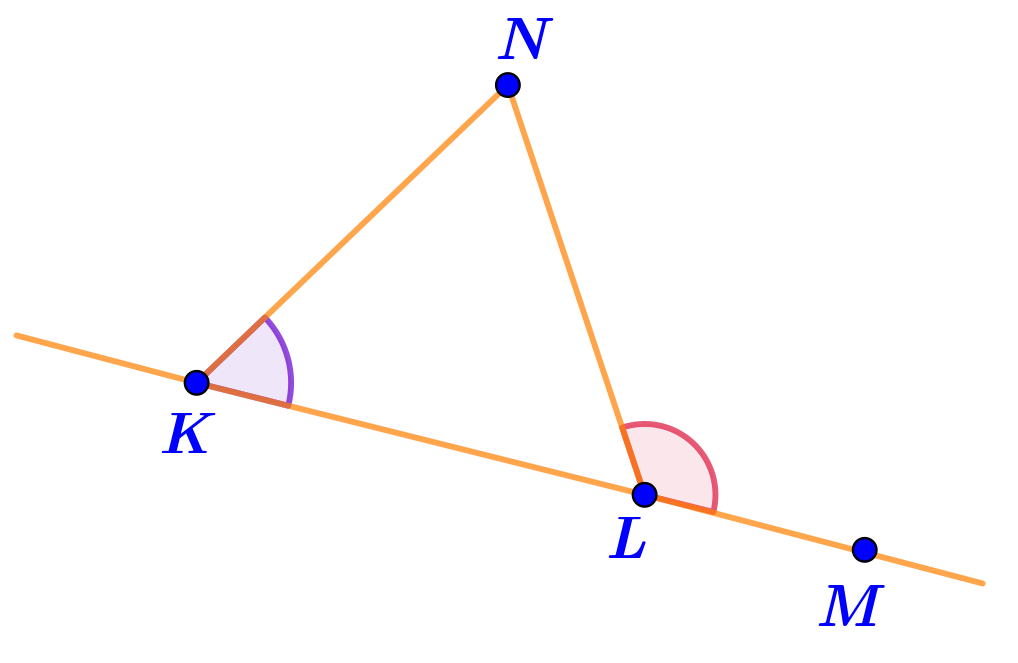
Найти длину отрезка \(\displaystyle KN{\small .}\)
\(\displaystyle KN=\)см.
Сумма величин смежных углов равна \(\displaystyle 180\degree {\small :}\)
\(\displaystyle \angle KLN+ \angle MLN=180\degree{\small .}\)
Величина одного из них известна:
\(\displaystyle \angle MLN=123\degree{\small .}\)
Выражаем величину другого:
\(\displaystyle \angle KLN= 180\degree- \angle MLN=180\degree -123\degree =57\degree {\small .}\)
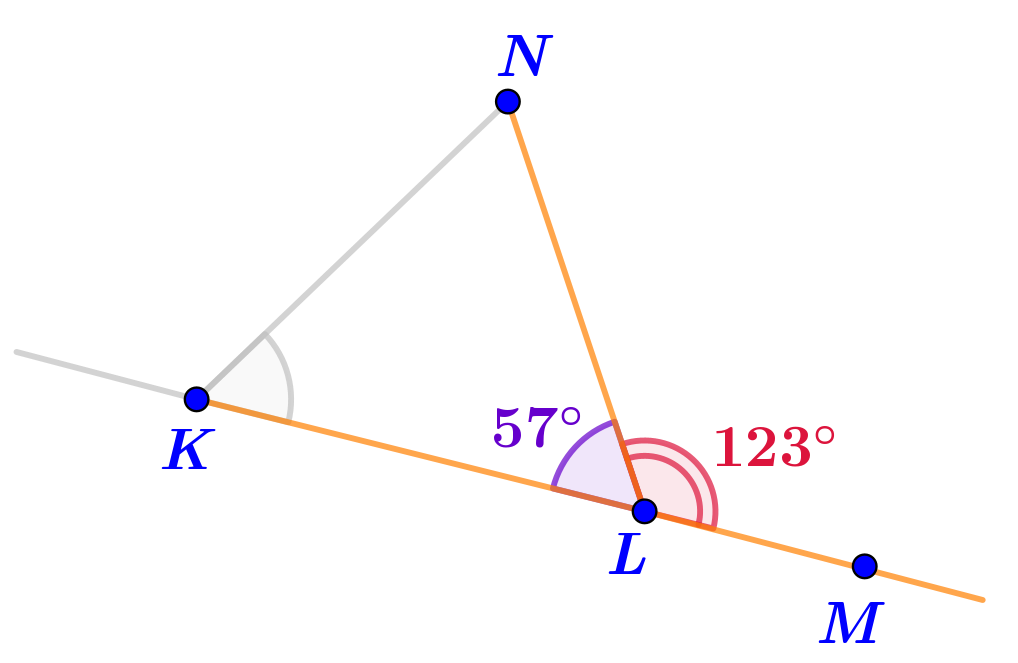
Найденная величина угла \(\displaystyle KLN\) оказалась равной величине угла \(\displaystyle LKN{\small .}\)
Значит эти углы равны:
\(\displaystyle \angle LKN=\angle KLN=57\degree\)
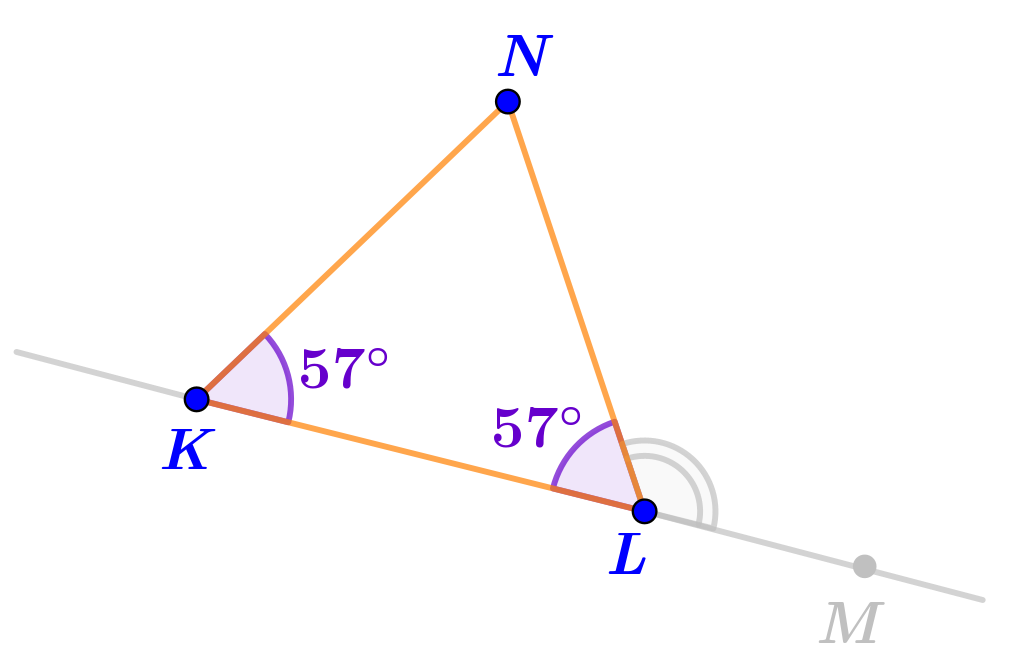
\(\displaystyle \angle LKN=\angle KLN=57\degree \quad\quad{\LARGE\Rightarrow}\quad\begin{array}{c} \\KN=LN\\\text{ \footnotesize\it(по признаку равнобедренного треугольника)}\end{array}\)
Искомая длина отрезка найдена:
\(\displaystyle KN=LN=12\, {\footnotesize cм}{\small.}\)
Ответ: \(\displaystyle 12\, {\footnotesize cм}{\small.}\)