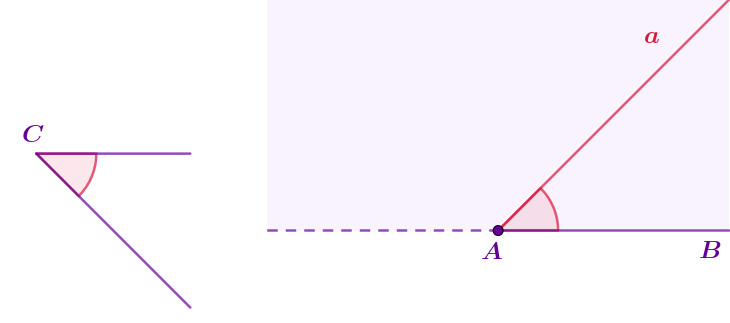
Величины трёх углов треугольника относятся друг к другу как \(\displaystyle 1:2:3\).
Длина медианы, проведённой из вершины самого большого угла, равна \(\displaystyle 4{\small .}\)
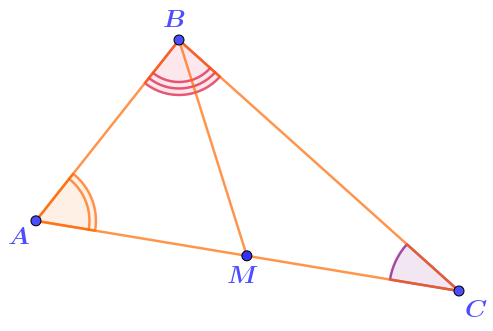
Найдите длину стороны, к которой проведена медиана.
\(\displaystyle AC=\)
Заметим, что данный треугольник можно "разрезать" на два треугольника так, чтобы каждый имел пару равных углов.
Тогда эти части \(\displaystyle -\) равнобедренные треугольники, и "линия разреза" \(\displaystyle -\) боковая сторона в каждом из них.
На рисунке "линия разреза" \(\displaystyle -\) медиана \(\displaystyle BM{\small .}\)
Но чтобы доказать это, приходится "разрезать" треугольник заново.
Вторая сторона отложенного угла пересечёт сторону \(\displaystyle AC\) в точке, которую мы обозначим через \(\displaystyle N{\small .}\)
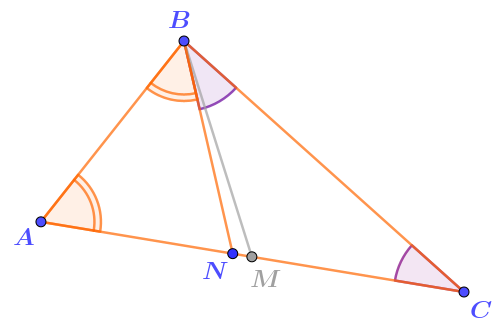
По условию, величина угла \(\displaystyle C\) составляет треть величины угла \(\displaystyle ABC{ \small ,}\) а величина угла \(\displaystyle A\; -\) две трети того же угла.
Углы \(\displaystyle C\) и \(\displaystyle CBN\) равны.
Значит, на долю угла \(\displaystyle ABN\) приходятся две трети величины угла \(\displaystyle ABC{\small :}\)
\(\displaystyle \angle ABN=\angle ABC-\angle CBN=\angle ABC-\frac{1}{3}\angle ABC=\frac{2}{3}\angle ABC=\angle A{\small .}\)
Боковые стороны этих треугольников противолежат равным углам:
\(\displaystyle AN=BN=CN\)
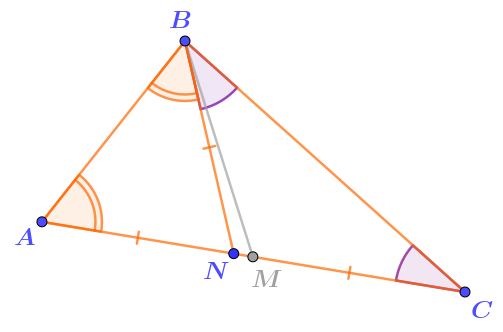
То есть точка \(\displaystyle N \;-\) середина отрезка \(\displaystyle AC{\small .}\)
Но по условию задачи серединой отрезка \(\displaystyle AC\) является точка \(\displaystyle M{\small .}\)
Значит, точки \(\displaystyle N\) и \(\displaystyle M\) совпадают, а длина стороны \(\displaystyle AC\) равна удвоенной длине медианы \(\displaystyle BM{\small :}\)
\(\displaystyle AC=AN+CN=2\cdot BN=2\cdot BM=2\cdot 4=8\)
Ответ: \(\displaystyle AC=8{\small .}\)