Задание
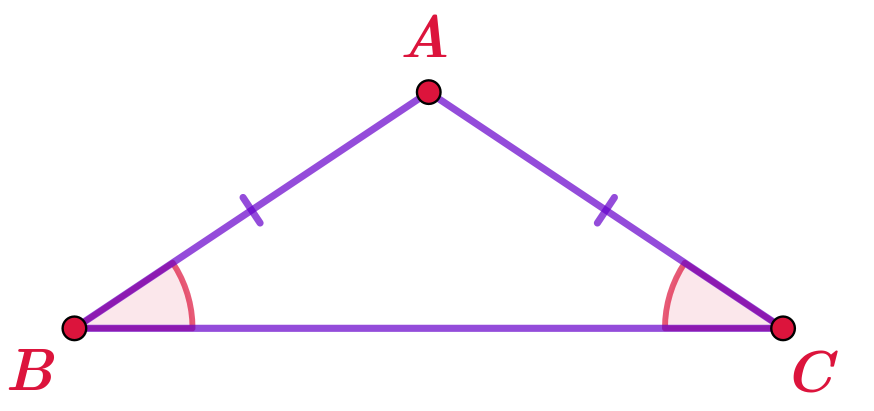
В треугольнике \(\displaystyle ABC\) с двумя равными углами провели биссектрису \(\displaystyle CK{\small .}\)
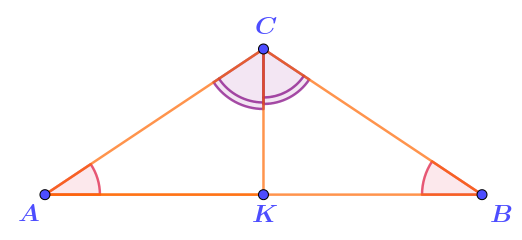
Дополните доказательство равенства отрезков \(\displaystyle AK\) и \(\displaystyle BK{\small .}\)
| \(\displaystyle 1.\;\;\;\;\) | \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle AC=BC\) |
| (по признаку равнобедренного треугольника) |
| \(\displaystyle 2.\;\;\;\; \left\{ \begin{array}{ll} \\ \\ \\ \\ \\ \\ \end{array} \right.\) | |||||
| \(\displaystyle CK\; -\) общая сторона | \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle AK=BK\) | ||
| (по первому признаку) |
Решение
1. Треугольник \(\displaystyle ABD\) равнобедренный по признаку равнобедренного треугольника.
На рисунке в треугольнике \(\displaystyle ABC\) отмечена пара равных углов:
\(\displaystyle \angle A = \angle B{\small .}\)
Значит, углы \(\displaystyle A \) и \(\displaystyle B\) — углы при основании \(\displaystyle AB\) равнобедренного треугольника \(\displaystyle ABC{\small .}\)
Тогда отрезки \(\displaystyle AC\) и \(\displaystyle BC\)— его боковые стороны и
\(\displaystyle AC=BC{\small .}\)
2. Треугольники \(\displaystyle ACK\) и \(\displaystyle BCK\) равны по двум сторонам и углу между ними.
| \(\displaystyle \left\{ \begin{array}{ll} \\ \\ \\ \\ \end{array} \right.\) | \(\displaystyle AC=BC\) | ||||
| \(\displaystyle CK\; -\) общая сторона | \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle {\bf\triangle}ACK={\bf\triangle}BCK\) | \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle AK=BK\) | |
| \(\displaystyle \angle ACK=\angle BCK\) | (по первому признаку) |
Ответ:
