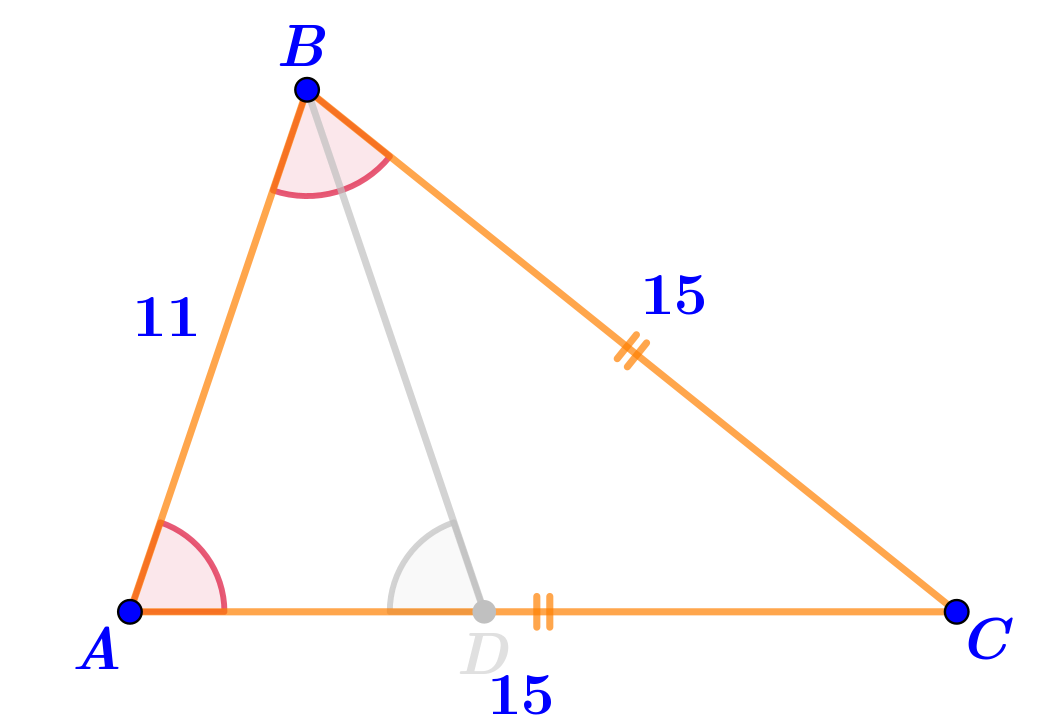
В треугольнике \(\displaystyle ABC\) на стороне \(\displaystyle AC\) отмечена точка \(\displaystyle D{\small .}\)
На рисунке отмечены три равных угла.
Известны длины отрезков: \(\displaystyle BD=11\)\(\displaystyle {\footnotesize см}\) и \(\displaystyle BC=15\)\(\displaystyle {\footnotesize см}{\small.}\)
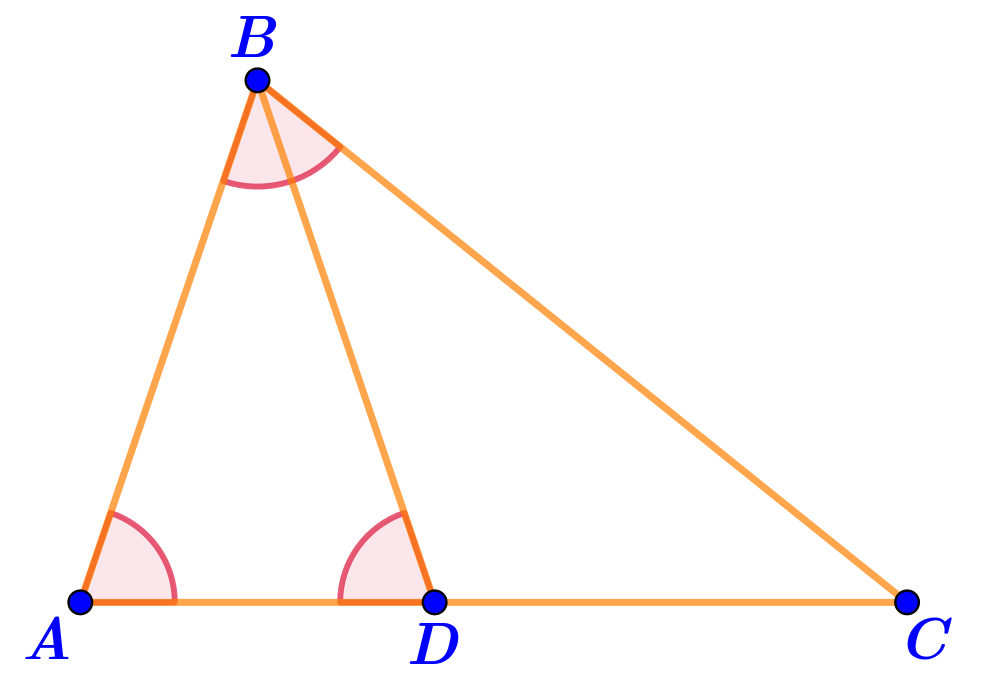
Найдите периметр треугольника \(\displaystyle ABC{\small .}\)
\(\displaystyle P_{ABC}=\)см.
\(\displaystyle P_{ABC}=AB+BC+AC{\small.}\)
Известна длина только одной стороны этого треугольника:
\(\displaystyle BC=15\,{\footnotesize см}{\small .}\)
Найдем длины сторон \(\displaystyle AB\) и \(\displaystyle AC{\small .}\)
На рисунке в треугольнике \(\displaystyle ABD\) отмечена пара равных углов:
\(\displaystyle \angle BAD = \angle BDA{\small .}\)
Значит, углы \(\displaystyle BAD \) и \(\displaystyle BDA\) — углы при основании \(\displaystyle AD\) равнобедренного треугольника \(\displaystyle ABD{\small }\)
Тогда отрезки \(\displaystyle AB=DB\) — его боковые стороны.
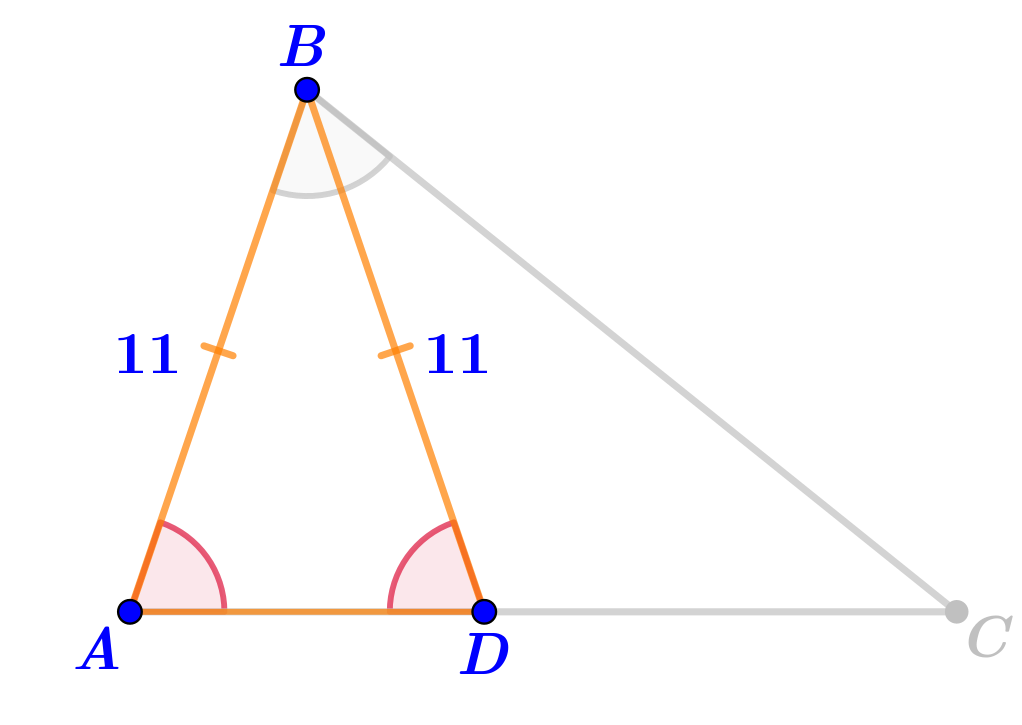
Сторона \(\displaystyle AB\) треугольника \(\displaystyle ABC\) найдена:
\(\displaystyle AB=DB=11\,{\footnotesize см}{\small .}\)
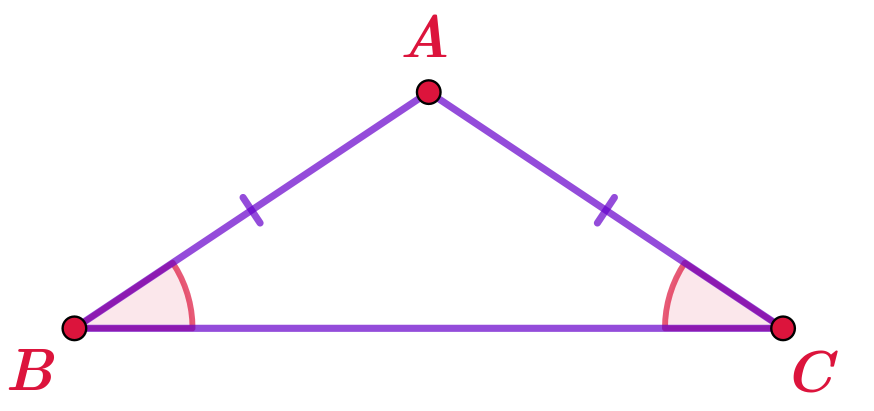
Равные углы прилежат к основанию \(\displaystyle AB\) равнобедренного треугольника \(\displaystyle ABC{\small .}\)
Боковыми сторонами являются отрезки \(\displaystyle AC=BC{\small .}\)
Сторона \(\displaystyle AC\) треугольника \(\displaystyle ABC\) найдена:
\(\displaystyle AC=BC=15\,{\footnotesize см}{\small .}\)
Все длины сторон найдены в одинаковых единицах:
\(\displaystyle AB=11\, {\footnotesize cм}{\small,}\)\(\displaystyle BC=AC=15\, {\footnotesize см}{\small .}\)
Периметр равен
\(\displaystyle P_{ABC}=11+15+15=41\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle 41\, {\footnotesize см}{\small.}\)