Задание
Найдите площадь треугольника, стороны которого равны \(\displaystyle 15\small,\) \(\displaystyle 16\) и \(\displaystyle 17\small.\)
Решение
Для нахождения площади треугольника воспользуемся формулой Герона.
Правило
Формула Герона
Площадь треугольника со сторонами \(\displaystyle a\small,\) \(\displaystyle b\) и \(\displaystyle c\) можно вычислить по формуле:
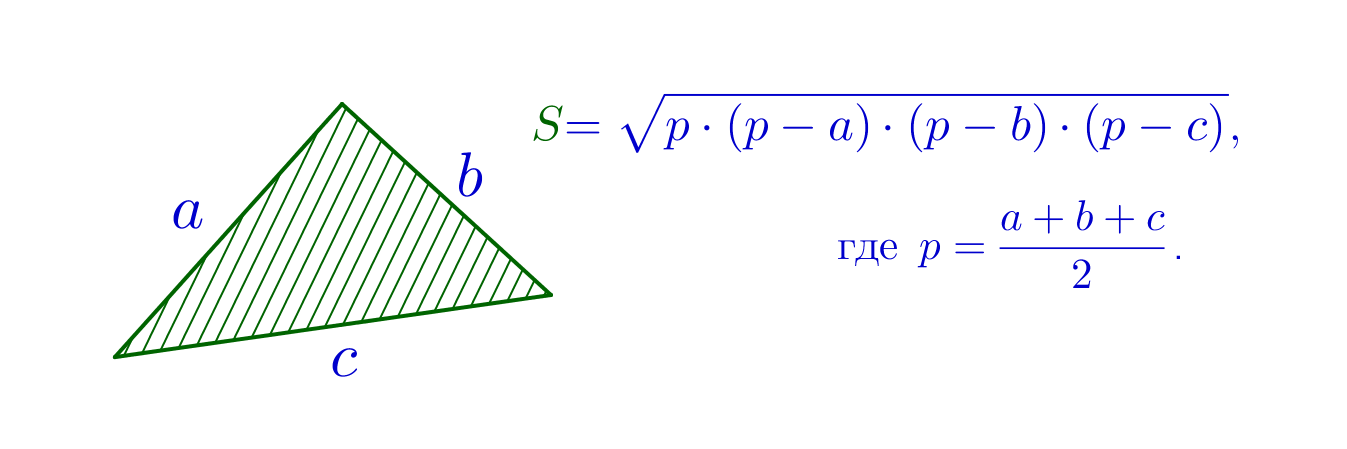
Вычислим полупериметр треугольника со сторонами \(\displaystyle 15\small,\) \(\displaystyle 16\) и \(\displaystyle 17\small{:}\)
\(\displaystyle p=\frac{15+16+17}{2}=24\small.\)
Подставим известные значения в формулу Герона и вычислим площадь треугольника:
\(\displaystyle S=\sqrt{24\cdot (24-15)\cdot (24-16)\cdot (24-17)}=\sqrt{24\cdot 9\cdot 8\cdot7}=24\sqrt{21}\small.\)
Ответ: \(\displaystyle 24\sqrt{21}\small.\)