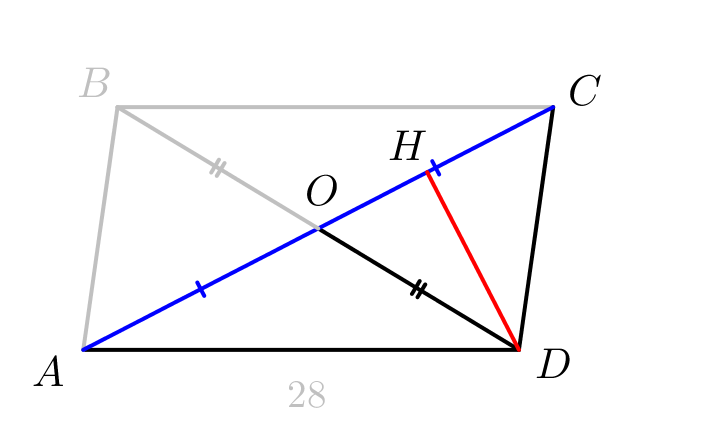
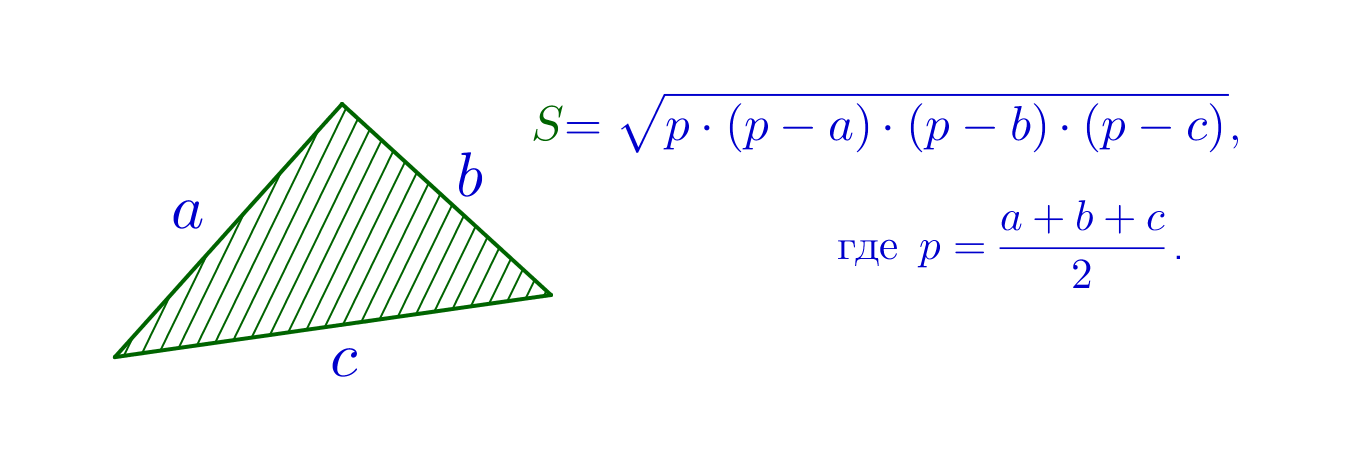Найдите площадь параллелограмма, если одна из его сторон равна \(\displaystyle 28\small,\) а диагонали равны \(\displaystyle 30\) и \(\displaystyle 34\small.\)
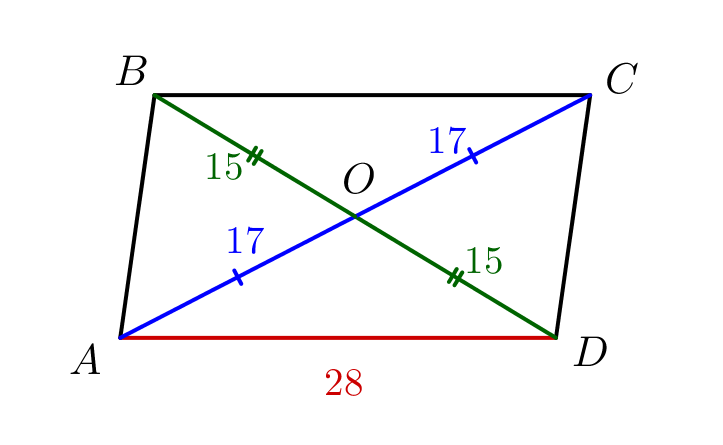
В параллелограмме \(\displaystyle ABCD\) известны следующие величины:
Диагонали параллелограмма точкой пересечения делятся пополам:
|  |
Диагонали разбивают параллелограмм на \(\displaystyle 4\) треугольника. Покажем, что площади всех четырех треугольников равны.
Рассмотрим треугольник \(\displaystyle ACD\small.\)
\(\displaystyle S_{AOD}=S_{COD}\small.\)
Рассматривая треугольники \(\displaystyle BCD\) и \(\displaystyle ABC{\small,}\) получаем:
\(\displaystyle S_{AOD}=S_{COD}=S_{COB}=S_{BOA}\small.\)
Значит, площадь параллелограмма \(\displaystyle ABCD\) в \(\displaystyle 4\) раза больше площади треугольника \(\displaystyle AOD\small{:}\)
\(\displaystyle S_{ABCD}=4\cdot S_{AOD}\small.\)
\(\displaystyle p=\frac{OD+AO+AD}{2}=\frac{15+17+28}{2}=30\small,\)
\(\displaystyle S_{AOD}=\sqrt{30\cdot (30-15)\cdot (30-17)\cdot (30-28)}=\sqrt{30\cdot 15\cdot 13\cdot 2}=30\sqrt{13}\small.\)
Тогда
\(\displaystyle S_{ABCD}=4\cdot S_{AOD}=120\sqrt{13}\small.\)
Ответ: \(\displaystyle 120\sqrt{13}\small.\)