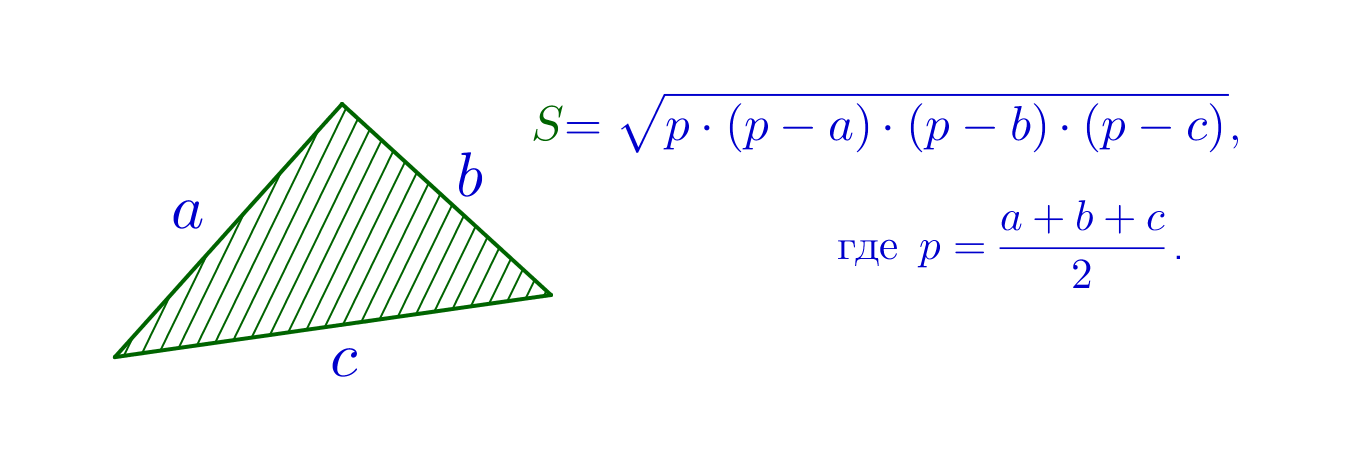Внутри треугольника \(\displaystyle ABC\) со сторонами \(\displaystyle AB=10,\,AC=21,\,BC=17\) отметили точку \(\displaystyle M\small.\) Оказалось, что расстояние от точки \(\displaystyle M\) до стороны \(\displaystyle AC\) равно \(\displaystyle 2\small,\) а до стороны \(\displaystyle BC\) равно \(\displaystyle 4\small.\) Найдите расстояние от точки \(\displaystyle M\) до прямой \(\displaystyle AB\small.\)
Соединим точку \(\displaystyle M\) с вершинами треугольника. Отметим, что длины высот получившихся треугольников и есть расстояния от точки \(\displaystyle M\) до соответствующих сторон. | 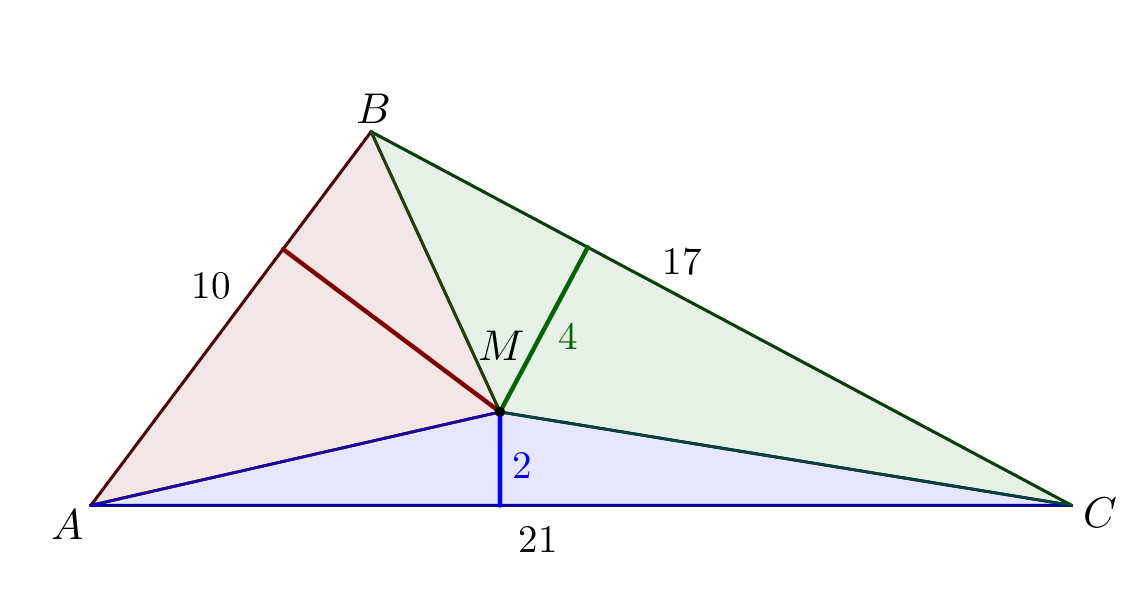 |
Треугольник \(\displaystyle ABC\) разбился на три треугольника: \(\displaystyle AMB,\,BMC\) и \(\displaystyle AMC\small.\) Тогда
\(\displaystyle S_{ABC}=S_{AMC}+S_{BMC}+S_{AMB}\small.\)
Высота треугольника \(\displaystyle AMB\) является расстоянием от точки \(\displaystyle M\) до стороны \(\displaystyle AB\small.\)
Поэтому, чтобы найти расстояние от точки \(\displaystyle M\) до стороны \(\displaystyle AB{\small:}\)
- найдем площади треугольников \(\displaystyle ABC,\,BMC\) и \(\displaystyle AMC\small,\)
- найдем площадь треугольника \(\displaystyle AMB\small,\)
- из площади треугольника \(\displaystyle AMB\) найдем его высоту.
Находим полупериметр:
\(\displaystyle p=\frac{10+21+17}{2}=24\)
Тогда
\(\displaystyle S_{ABC}=\sqrt{24\cdot(24-10)(24-21)(24-17)}=\sqrt{24\cdot14\cdot3\cdot7}=84\small.\)
Найдем площади треугольников \(\displaystyle BMC\) и \(\displaystyle AMC\small.\) Для этого воспользуемся тем, что площадь треугольника равна половине произведения основания на высоту:
| 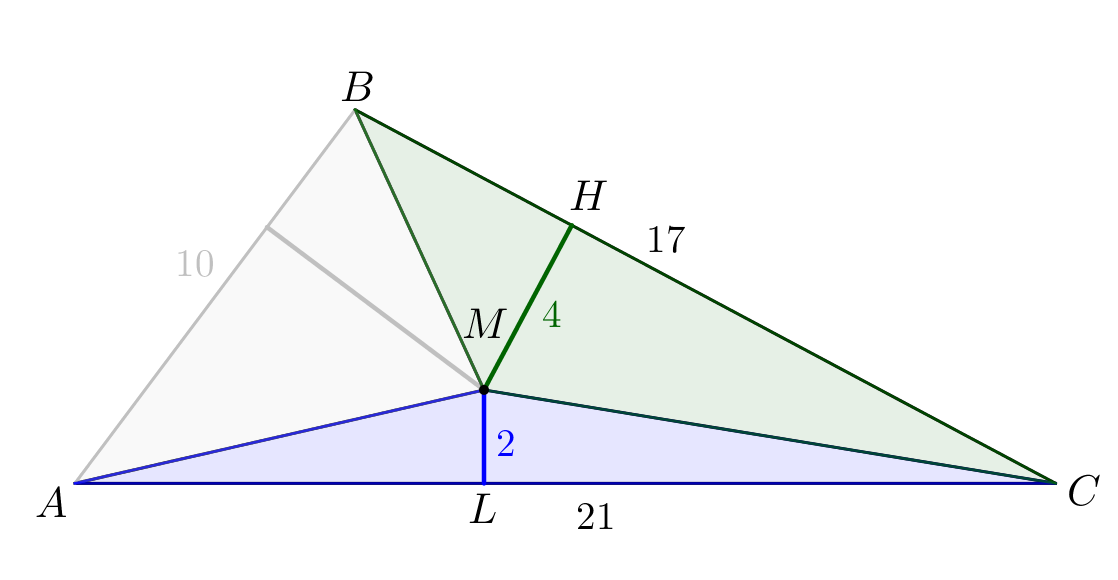 |
2. Найдем площадь треугольника \(\displaystyle AMB\small.\)
Для этого подставим в формулу известные значения площадей \(\displaystyle ABC,\,BMC\) и \(\displaystyle AMC{\small:}\)
\(\displaystyle S_{ABC}=S_{AMC}+S_{BMC}+S_{AMB}\small,\)
\(\displaystyle 84=21+34+S_{AMB}\small.\)
Значит,
\(\displaystyle S_{AMB}=84-21-34=29\small.\)
3. Найдем высоту треугольника \(\displaystyle AMB\small.\)
Площадь треугольника равна половине произведения основания на высоту. Тогда, если обозначить высоту треугольника \(\displaystyle AMB\) за \(\displaystyle h\small,\) то \(\displaystyle S_{AMB}=\frac{AB\cdot h}{2}\small,\) \(\displaystyle 29=\frac{10h}{2}\small,\) \(\displaystyle h=5{,}8\small.\) | 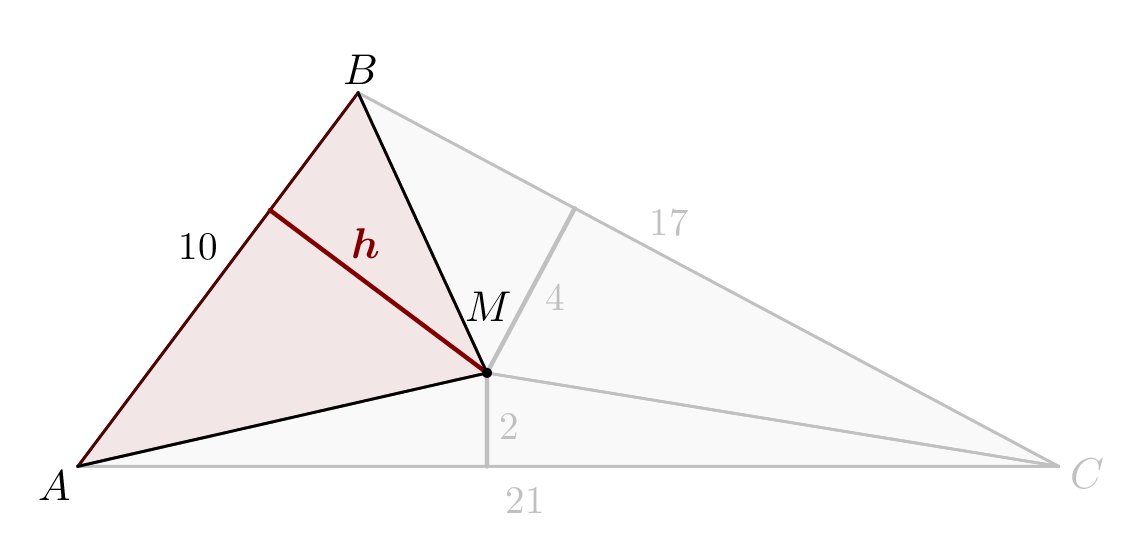 |
Ответ: \(\displaystyle h=5{,}8\small.\)