Найдите площадь трапеции с основаниями \(\displaystyle 54\) и \(\displaystyle 18\) и боковыми сторонами \(\displaystyle 21\) и \(\displaystyle 33\small.\)
Основания трапеции:
Боковые стороны:
| 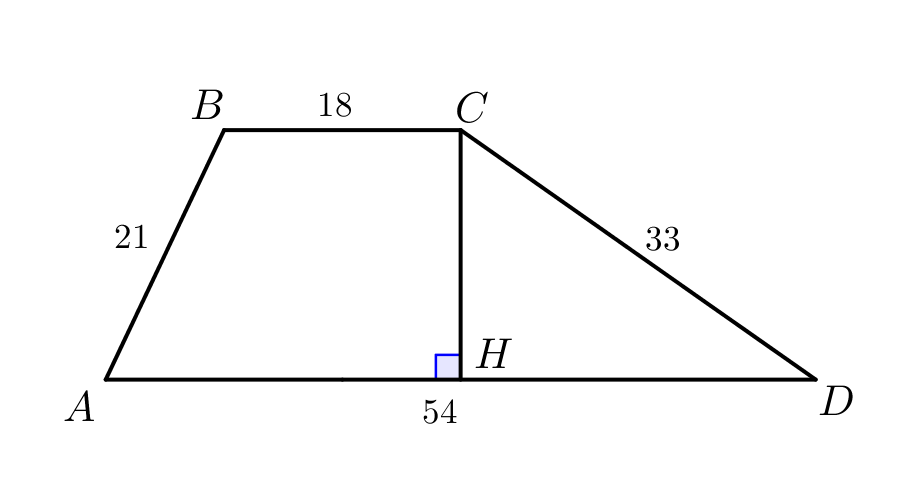 |
Построим треугольник с известными сторонами, для которого \(\displaystyle CH\) будет высотой. Через точку \(\displaystyle C\) проведем прямую, параллельную стороне \(\displaystyle AB\small,\) до пересечения с основанием \(\displaystyle AD\) в точке \(\displaystyle K\small.\) | 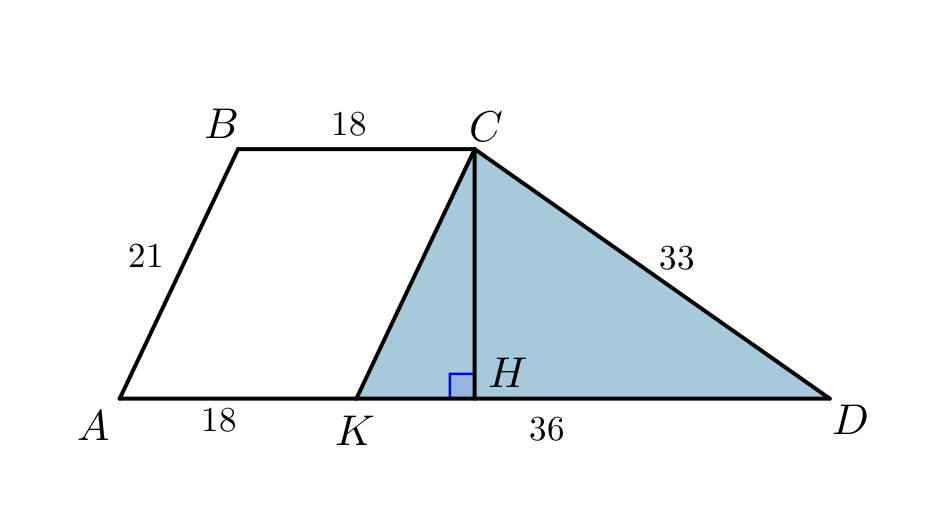 |
Высота трапеции \(\displaystyle CH\) является высотой треугольника \(\displaystyle CKD\small,\) стороны которого известны:
\(\displaystyle CK=21\small,\) \(\displaystyle CD=33\small,\) \(\displaystyle KD=AD-BC=36\small.\)
- через формулу Герона
- и произведение высоты \(\displaystyle CH \) на основание \(\displaystyle KD{\small .} \)
\(\displaystyle p=\frac{CK+CD+KD}{2}=\frac{21+33+36}{2}=45\small,\)
\(\displaystyle S_{CKD}=\sqrt{45\cdot (45-21)\cdot (45-33)\cdot (45-36)}=\sqrt{45\cdot24\cdot12\cdot9}=108\sqrt{10}\small.\)
Найдем площадь треугольника \(\displaystyle CKD\) как произведение половины основания на высоту:
\(\displaystyle S=\frac{1}{2}\cdot KD\cdot CH\small.\)
Выразим \(\displaystyle CH\small{:}\)
\(\displaystyle CH=\frac{2S}{KD}=\frac{2\cdot108\sqrt{10}}{36}=6\sqrt{10}\small.\)
\(\displaystyle S=\frac{AD+BC}{2}\cdot CH=\frac{54+18}{2}\cdot 6\sqrt{10}=216\sqrt{10}\small.\)
Ответ:\(\displaystyle 216\sqrt{10}\small.\)