В параллелограмме угол \(\displaystyle A\) равен \(\displaystyle 60^{\circ}\) и сторона \(\displaystyle AB=4\small.\) Биссектриса угла \(\displaystyle A\) пересекает сторону \(\displaystyle BC\) в точке \(\displaystyle E\small.\) Найдите площадь треугольника \(\displaystyle ABE\small.\)
| 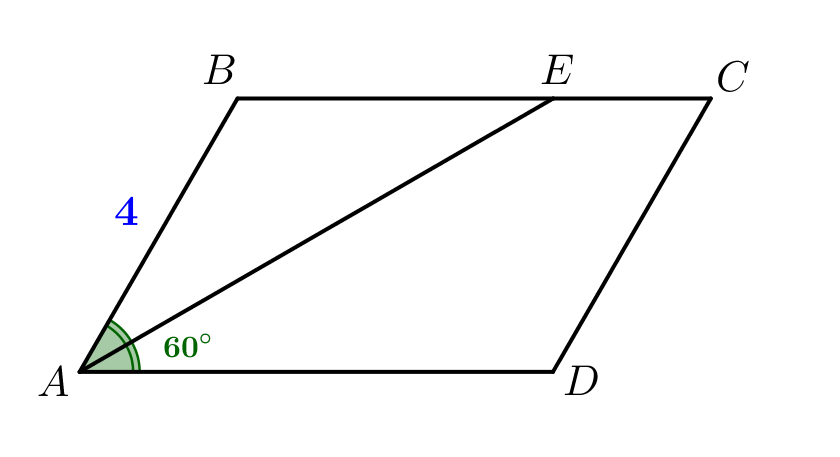 |
Биссектриса делит угол \(\displaystyle A\) пополам, то есть \(\displaystyle \angle BAE=\angle DAE = 30^{\circ}\small.\) Противоположные стороны параллелограмма параллельны, тогда накрест лежащие углы равны: \(\displaystyle \angle AEB=\angle DAE=30^{\circ}\small.\) |  |
Тогда треугольник \(\displaystyle ABE\) равнобедренный и \(\displaystyle AB=BE\small.\) А его последний угол \(\displaystyle B\) равен \(\displaystyle \angle B=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}\small.\) | 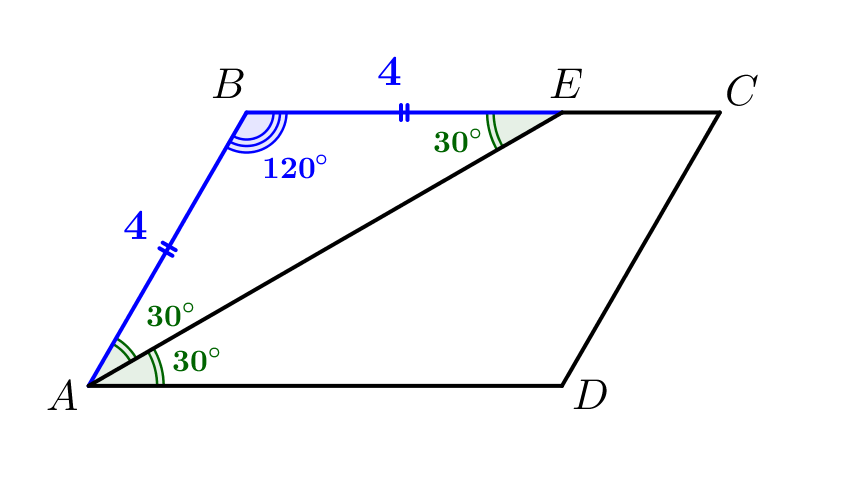 |
Найдем площадь треугольника, используя правило:
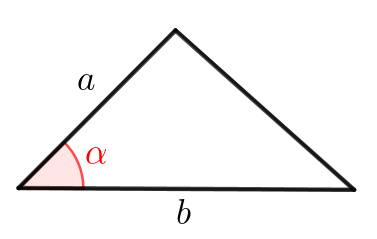
Формула площади треугольника через две стороны и угол между ними
Площадь треугольника со сторонами \(\displaystyle a,\,b\) и углом \(\displaystyle \color{red}{\alpha}\) между ними равна \(\displaystyle \frac{1}{2}ab\sin\color{red}{\alpha}\small.\)
Подставляя известные значения, получаем:
\(\displaystyle S_{ABE}=\frac{1}{2}\cdot4\cdot4\cdot\sin120^{\circ}=8\cdot\frac{\sqrt{3}}{2}=4\sqrt{3}\small.\)
Ответ: \(\displaystyle S_{ABE}=4\sqrt{3}\small.\)