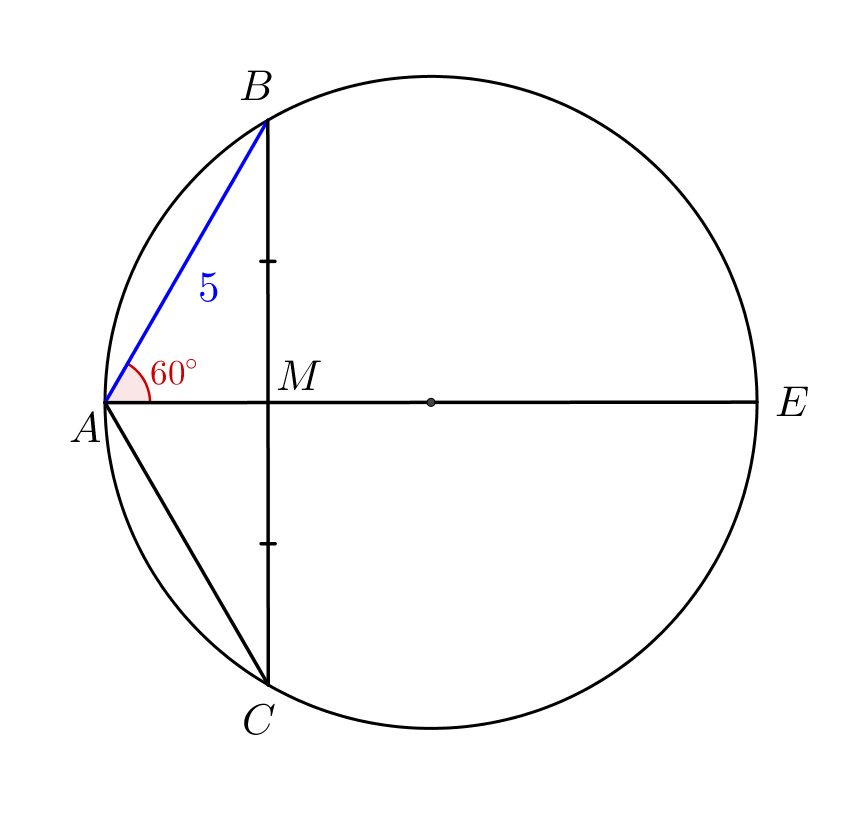
Вокруг треугольника \(\displaystyle ABC\) описана окружность. Продолжение медианы \(\displaystyle AM\) пересекает окружность в точке \(\displaystyle E\small.\) Известно, что \(\displaystyle AB=5,\,ME=AB+AM\) и \(\displaystyle \angle BAM=60^{\circ}\small.\) Найдите площадь треугольника \(\displaystyle ABC\small.\)
Дано:
|  |
На продолжении отрезка \(\displaystyle EA\) за точку \(\displaystyle A\) отметим точку \(\displaystyle D\) так, что \(\displaystyle AD=AB\small.\) Рассмотрим четырехугольник \(\displaystyle DBEC\small.\) Поскольку \(\displaystyle ME=AB+AM=AD+AM=MD\small,\) то в четырехугольнике \(\displaystyle DBEC\) диагонали делятся точкой пересечения пополам. | 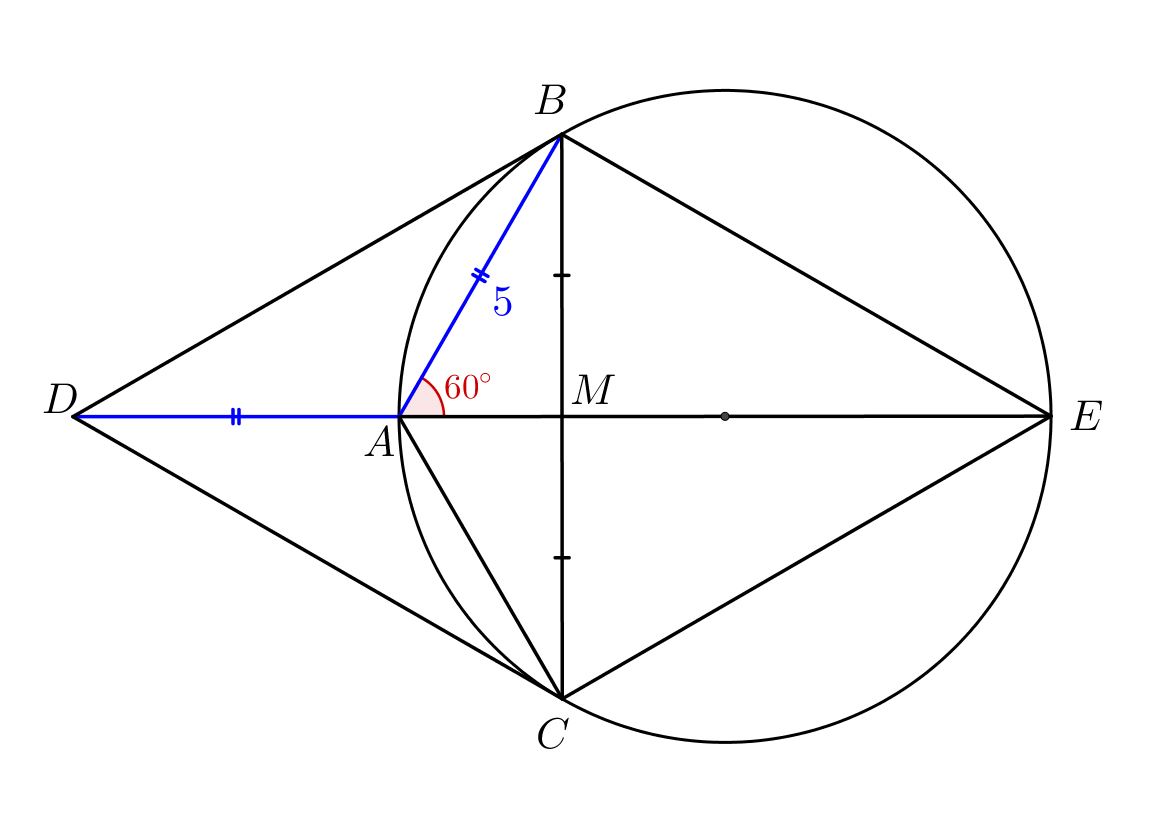 |
Значит, в треугольнике \(\displaystyle ABC\) отрезок \(\displaystyle AM\) – медиана и высота. То есть этот треугольник равнобедренный, а \(\displaystyle AM\) еще и биссектриса:
- \(\displaystyle AC=AB=5\small,\)
- \(\displaystyle \angle MAC=60^{\circ}\small.\)
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot AB\cdot AC\cdot\angle BAC=\frac{1}{2}\cdot5\cdot5\cdot\sin(60^{\circ}+60^{\circ})=\frac{25\sqrt{3}}{4}\small.\)
Ответ: \(\displaystyle S_{ABC}=\frac{25\sqrt{3}}{4}\small.\)