Окружность, вписанная в треугольник, делит точкой касания одну из сторон на отрезки \(\displaystyle 3\) и \(\displaystyle 4\small.\) Противолежащий этой стороне угол равен \(\displaystyle 120^{\circ}\small.\) Найдите площадь треугольника.
Отрезки касательных, проведенные из одной точки, равны. Обозначим \(\displaystyle AK=x\small,\) получаем:
| 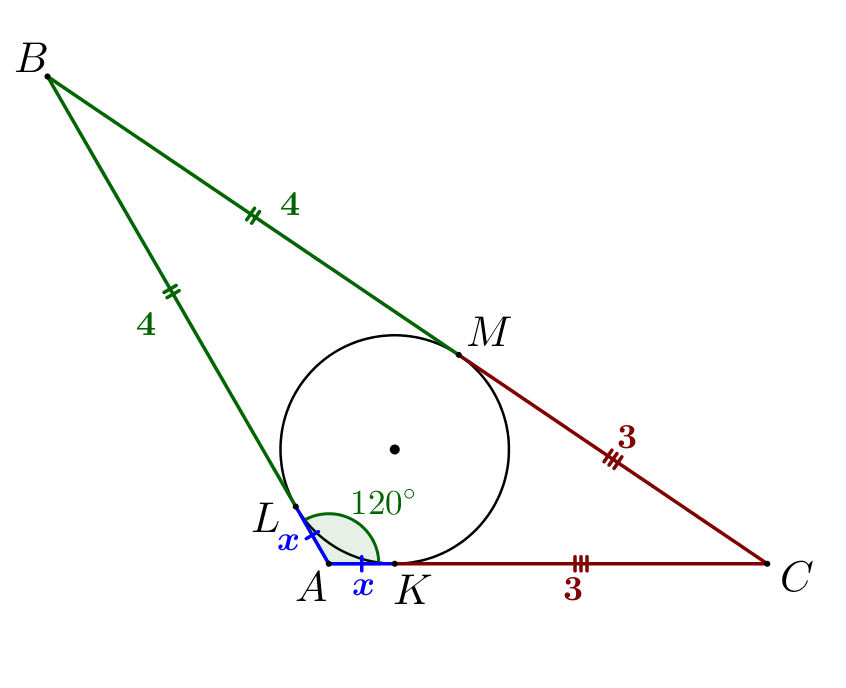 |
Используя теорему косинусов, найдем \(\displaystyle x\small.\)
Запишем теорему косинусов для треугольника \(\displaystyle ABC{\small:}\)
\(\displaystyle BC^2=AB^2+AC^2-2\cdot AB\cdot AC\cdot\cos \angle BAC\small.\)
Подставим известные значения:
\(\displaystyle (3+4)^2=(4+x)^2+(3+x)^2-2\cdot(4+x)(3+x)\cos120^{\circ}\small.\)
\(\displaystyle x^2+7x-4=0\small.\)
\(\displaystyle x_1=\frac{-7+\sqrt{65}}{2}\) и \(\displaystyle x_2=\frac{-7-\sqrt{65}}{2}\small.\)
Поскольку длина отрезка положительна, то
\(\displaystyle AK=AL=x=\frac{-7+\sqrt{65}}{2}\small.\)
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot AB\cdot AC\cdot\sin\angle A=8\sqrt{3}\small.\)
Воспользуемся правилом:
Формула площади треугольника через две стороны и угол между ними
Площадь треугольника со сторонами \(\displaystyle a,\,b\) и углом \(\displaystyle \color{red}{\alpha}\) между ними равна \(\displaystyle \frac{1}{2}ab\sin\color{red}{\alpha}\small.\)
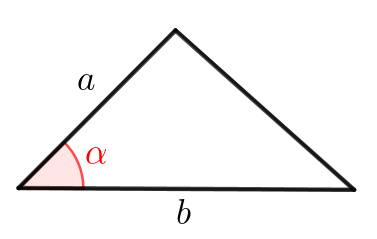
В данном случае
- \(\displaystyle AB=AL+LB=\frac{-7+\sqrt{65}}{2}+4=\frac{1+\sqrt{65}}{2},\)
- \(\displaystyle AC=AK+KC=\frac{-7+\sqrt{65}}{2}+3=\frac{-1+\sqrt{65}}{2},\)
- \(\displaystyle \sin\angle A=\sin120^{\circ}=\frac{\sqrt{3}}{2}.\)
Подставляя значения в формулу, получаем:
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot\frac{1+\sqrt{65}}{2}\cdot\frac{-1+\sqrt{65}}{2}\cdot\frac{\sqrt{3}}{2}=\frac{((\sqrt{65})^2-1^2)\cdot\sqrt{3}}{16}=4\sqrt{3}\small.\)
Ответ: \(\displaystyle S_{ABC}=4\sqrt{3}\small.\)