В треугольнике \(\displaystyle ABC\) известны стороны: \(\displaystyle AB=5,\,BC=7\small.\) Найдите биссектрису этого треугольника \(\displaystyle BL\small,\) если \(\displaystyle \angle ABC=60^{\circ}\small.\)
Биссектриса \(\displaystyle BL\) угла \(\displaystyle ABC\) делит его пополам, тогда \(\displaystyle \angle ABL=\angle CBL=\frac{60^{\circ}}{2}=30^{\circ}\small.\) Треугольник \(\displaystyle ABC\) состоит из двух треугольников: \(\displaystyle ABL\) и \(\displaystyle CBL\small.\) Значит, \(\displaystyle S_{ABC}=\color{blue}{S_{ABL}}+\color{green}{S_{CBL}}\small.\) | 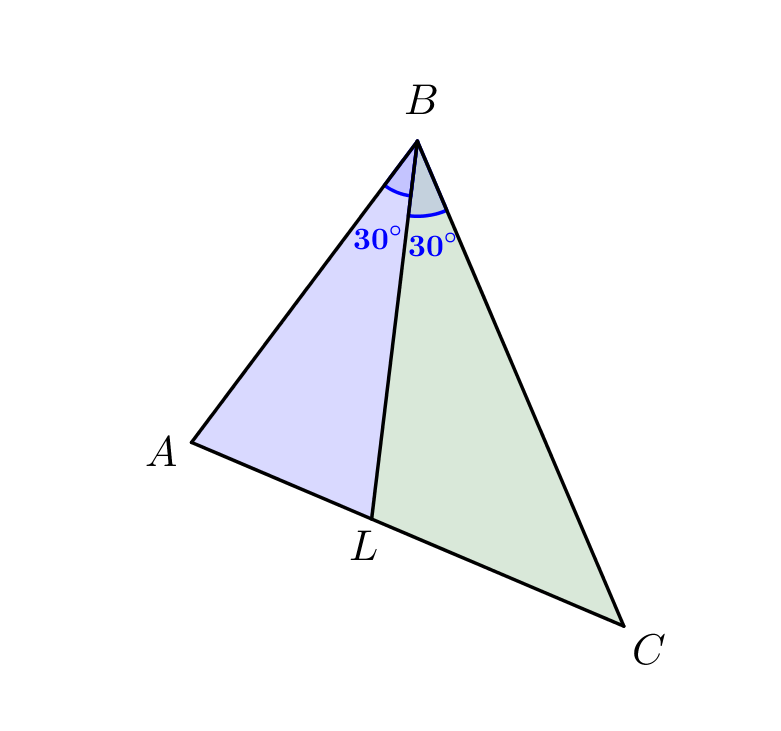 |
Тогда, используя правило, выразим площадь каждого треугольника через известные элементы и \(\displaystyle BL\small.\)
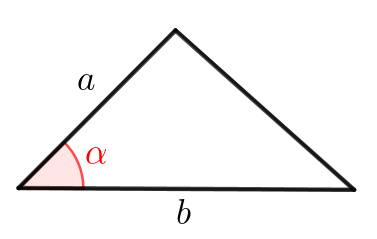
Формула площади треугольника через две стороны и угол между ними
Площадь треугольника со сторонами \(\displaystyle a,\,b\) и углом \(\displaystyle \color{red}{\alpha}\) между ними равна \(\displaystyle \frac{1}{2}ab\sin\color{red}{\alpha}\small.\)
Площадь треугольника \(\displaystyle ABC{\small:}\)
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot AB \cdot BC\cdot \sin60^{\circ}=\frac{1}{2}\cdot5\cdot7\cdot\frac{\sqrt{3}}{2}=\frac{35\sqrt{3}}{4}\small. \)
Площадь треугольника \(\displaystyle ABL{\small:}\)
\(\displaystyle S_{ABL}=\frac{1}{2}\cdot AB \cdot BL\cdot \sin30^{\circ}=\frac{1}{2}\cdot5\cdot BL\cdot\frac{1}{2}=\frac{5}{4}BL\small. \)
Площадь треугольника \(\displaystyle CBL{\small:}\)
\(\displaystyle S_{CBL}=\frac{1}{2}\cdot CB \cdot BL\cdot \sin30^{\circ}=\frac{1}{2}\cdot7\cdot BL\cdot\frac{1}{2}=\frac{7}{4}BL\small. \)
Теперь подставим результаты в выражение \(\displaystyle S_{ABC}=S_{ABL}+S_{CBL}{\small,}\) получаем:
\(\displaystyle \frac{35\sqrt{3}}{4}=\frac{5}{4}BL+\frac{7}{4}BL\small.\)
Найдем \(\displaystyle BL{\small:}\)
\(\displaystyle \frac{35\sqrt{3}}{4}=\frac{12}{4}BL=3BL\small,\)
\(\displaystyle BL=\frac{35\sqrt{3}}{4}:3=\frac{35\sqrt{3}}{12}\small.\)
Ответ: \(\displaystyle BL=\frac{35\sqrt{3}}{12}\small.\)