На клетчатой бумаге с размером клетки \(\displaystyle 1{\footnotesize см}×1{\footnotesize см}\) изображён четырёхугольник \(\displaystyle ABCD{\small.}\)
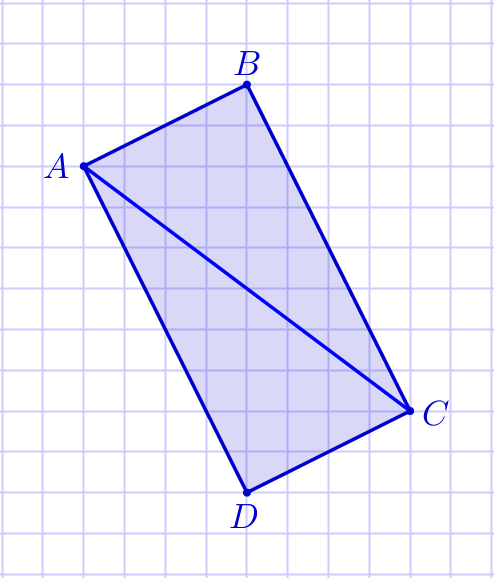
\(\displaystyle \color{red}{1{\small.}}\) Является ли данный четырёхугольник \(\displaystyle ABCD\) прямоугольником?
\(\displaystyle \color{red}{2{\small.}}\) Найдите длину диагонали \(\displaystyle AC{\small.}\) Ответ запишите в сантиметрах.
\(\displaystyle AC=\) \(\displaystyle {\footnotesize см}{\small.}\)
\(\displaystyle \color{red}{1{\small.}}\) Выясним, является ли данный четырёхугольник \(\displaystyle ABCD\) прямоугольником.
Выполним дополнительные построения.
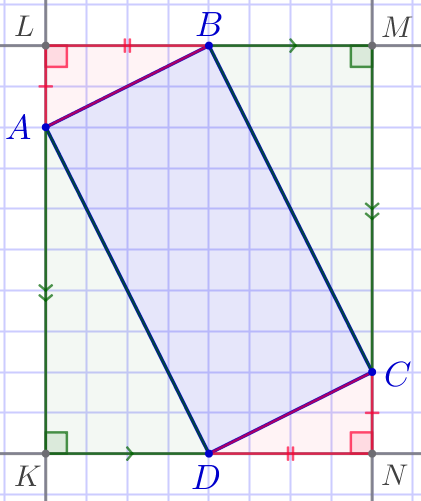
Впишем данный четырёхугольник \(\displaystyle ABCD\) в прямоугольник \(\displaystyle KLMN{\small,}\) образованный линиями сетки. | 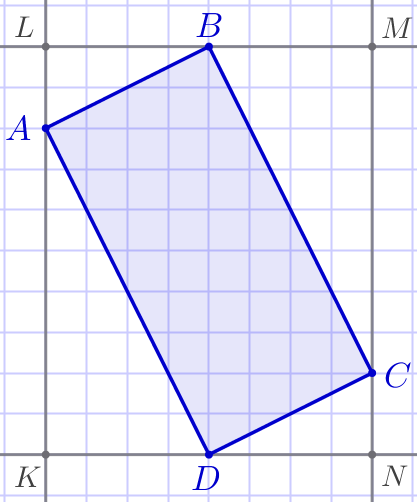 |
Рассмотрим прямоугольные треугольники \(\displaystyle ALB{\small,}\) \(\displaystyle BMC{\small,}\) \(\displaystyle CND{\small,}\) \(\displaystyle AKD{\small.}\)
 |
Следовательно, гипотенузы этих треугольников равны: \(\displaystyle \color{blue}{AB}=\color{blue}{CD}{\small.}\)
Следовательно, гипотенузы этих треугольников равны: \(\displaystyle \color{blue}{AD}=\color{blue}{BC}{\small.}\) |
В четырёхугольнике \(\displaystyle ABCD\) противоположные стороны попарно равны.
\(\displaystyle ABCD\) – параллелограмм.
Выясним, является ли параллелограмм \(\displaystyle ABCD\) прямоугольником.
Определим величину угла \(\displaystyle B{\small.}\)
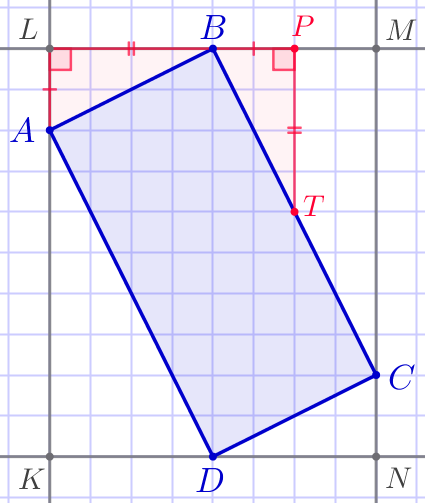 | На прямой \(\displaystyle LM\) отметим точку \(\displaystyle P\) так, что \(\displaystyle BP=AL{\small.}\) Из точки \(\displaystyle P\) опустим перпендикуляр к отрезку \(\displaystyle BC{\small.}\) Точку пересечения обозначим буквой \(\displaystyle T{\small.}\) По рисунку видим, что \(\displaystyle PT=LB{\small.}\) В результате получаем \(\displaystyle \color{red}{\triangle ALB}=\color{red}{ \triangle BPT}\) – по двум катетам. |
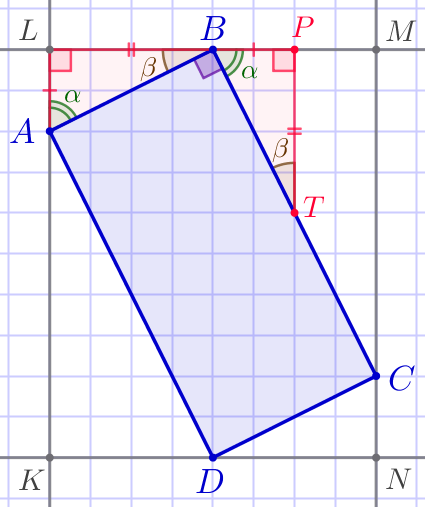 | В равных треугольниках соответственные углы равны: \(\displaystyle \angle LAB=\angle PBT=\color{green}{\alpha}{\small,}\) \(\displaystyle \angle LBA=\angle PTB=\color{brown}{\beta}{\small.}\) Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small,}\) то есть \(\displaystyle \color{green}{\alpha}+\color{brown}{\beta}=90^{\circ}{\small.} \) Тогда \(\displaystyle \angle B=180^{\circ}-(\color{green}{\alpha}+\color{brown}{\beta})=180^{\circ}-90^{\circ}=90^{\circ}{\small.}\) |
Значит,
\(\displaystyle \angle A=\angle B=\angle C=\angle D=90^{\circ}{\small.}\)
\(\displaystyle ABCD\) – прямоугольник.
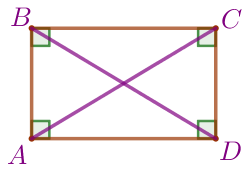
\(\displaystyle \color{red}{2{\small.}}\) Найдём длину диагонали \(\displaystyle AC{\small.}\)
\(\displaystyle AC=BD{\small.}\)
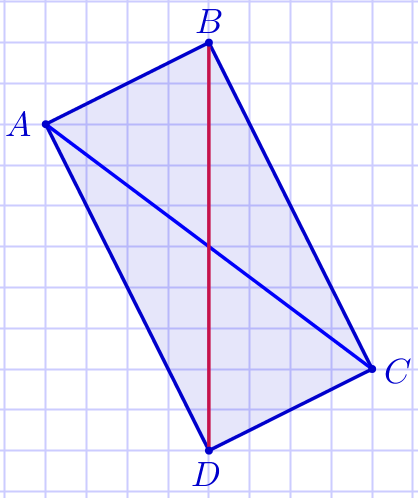 | В прямоугольнике \(\displaystyle ABCD\) проведём диагональ \(\displaystyle BD{\small.}\) Посчитаем длину диагонали \(\displaystyle BD\) по клеткам. \(\displaystyle BD=10\) клеток. Сторона клетки равна \(\displaystyle 1\, \footnotesize см{\small.}\) Значит, \(\displaystyle BD=10\, \footnotesize см{\small.}\) Следовательно, \(\displaystyle AC=10\, \footnotesize см{\small.}\) |
| Ответ: | \(\displaystyle \color{red}{1{\small.}}\) Является ли данный четырёхугольник \(\displaystyle ABCD\) прямоугольником? Да. |
| \(\displaystyle \color{red}{2{\small.}}\) \(\displaystyle AC=10\, \footnotesize см{\small.}\) |