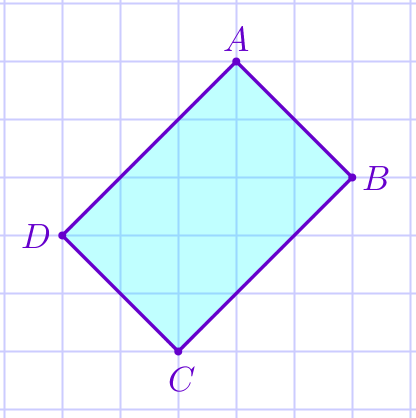
На клетчатой бумаге изображён четырёхугольник \(\displaystyle ABCD{\small.}\) Является ли данный четырёхугольник прямоугольником?
Выполним дополнительные построения.
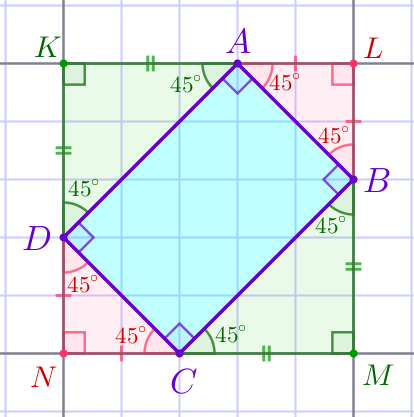
Впишем данный четырёхугольник \(\displaystyle ABCD\) в прямоугольник \(\displaystyle KLMN{\small,}\) образованный линиями сетки. | 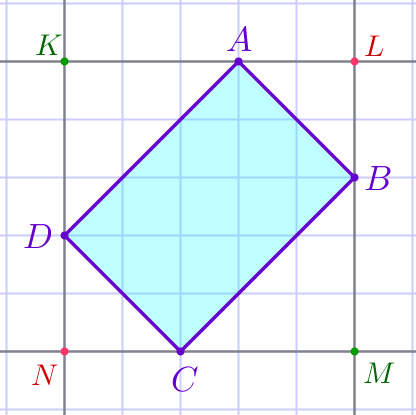 |
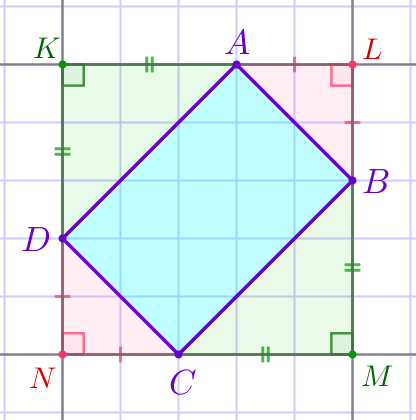
Рассмотрим прямоугольные треугольники \(\displaystyle ALB{\small,}\) \(\displaystyle BMC{\small,}\) \(\displaystyle CND{\small,}\) \(\displaystyle AKD{\small.}\)
 |
\(\displaystyle \color{blue}{AB}=\color{blue}{CD}{\small.}\)
\(\displaystyle \color{blue}{AD}=\color{blue}{BC}{\small.}\) |
В четырёхугольнике \(\displaystyle ABCD\) противоположные стороны попарно равны.
\(\displaystyle ABCD\) – параллелограмм.
Треугольники \(\displaystyle ALB{\small,}\) \(\displaystyle BMC{\small,}\) \(\displaystyle CND{\small,}\) \(\displaystyle AKD\) – прямоугольные и равнобедренные.
Значит, острые углы этих треугольников равны по \(\displaystyle 45^{\circ}{\small.}\) Тогда
 |
|
\(\displaystyle ABCD\) – прямоугольник.
Ответ: Да.