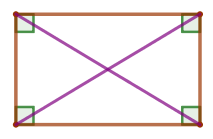
Диагонали \(\displaystyle AC\) и \(\displaystyle BD\) параллелограмма \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle O{\small,}\) \(\displaystyle AC=27\, {\footnotesize см}{\small,}\) \(\displaystyle BO=13{,}5\, {\footnotesize см}{\small,}\) \(\displaystyle OD=13{,}5\, {\footnotesize см}{\small.}\) Найдите угол \(\displaystyle ABD{\small,}\) если \(\displaystyle \angle CBD=36^{\circ}{\small.}\)
\(\displaystyle \angle ABD=\) \(\displaystyle ^{\circ}{\small.}\)
\(\displaystyle ABCD\) – параллелограмм:
| 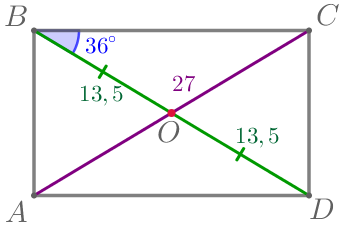 |
Требуется найти \(\displaystyle \angle ABD{\small.}\)
По условию, \(\displaystyle BO=OD=13{,}5\, \footnotesize см{\small,}\) тогда
\(\displaystyle BD=BO+OD=13{,}5+13{,}5=27\, \footnotesize см{\small.}\)
Получаем:
\(\displaystyle BD=AC=27\, \footnotesize см{\small.}\)
То есть диагонали параллелограмма \(\displaystyle ABCD\) равны.
\(\displaystyle ABCD\) – прямоугольник.
По определению, в прямоугольнике все углы прямые. При этом \(\displaystyle \color{green}{\angle ABC}=\color{red}{\angle ABD}+\color{blue}{ \angle CBD}{\small.}\) Выразим угол \(\displaystyle ABD{\small:}\) \(\displaystyle \color{red}{\angle ABD}=\color{green}{\angle ABC}- \color{blue}{ \angle CBD}{\small.}\) Подставим \(\displaystyle \angle ABC=90^{\circ}{\small,}\) \(\displaystyle \angle CBD=36^{\circ}{\small:}\) \(\displaystyle \color{red}{\angle ABD}=\color{green}{90^{\circ}}-\color{blue}{36^{\circ}}=\color{red}{54^{\circ}}{\small.}\) | 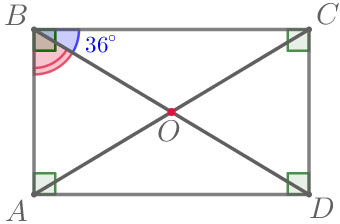 |
Ответ: \(\displaystyle \angle ABD=54^{\circ}{\small.}\)