Укажите верное утверждение.
Рассмотрим каждое утверждение:
верно
| Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. | 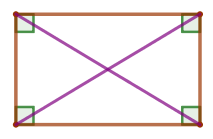 |
Согласно признаку прямоугольника данное утверждение верно.
неверно
Утверждение является верным, если оно верно во всех случаях.
Однако не каждый четырёхугольник с равными диагоналями является прямоугольником. Например,
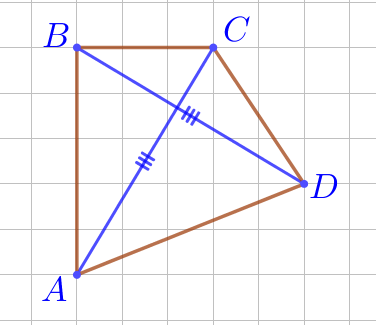 | \(\displaystyle \color{blue}{AC}=\color{blue}{BD}{\small,}\) \(\displaystyle \angle A \,\cancel=\, 90^{\circ}{\small,}\) \(\displaystyle \angle C \,\cancel=\, 90^{\circ}{\small,}\) \(\displaystyle \angle D \,\cancel=\, 90^{\circ}{\small.}\) \(\displaystyle ABCD\) – не прямоугольник. |
Следовательно, данное утверждение неверно.
неверно
Утверждение является верным, если оно верно во всех случаях.
Однако не каждый четырёхугольник, у которого два противоположных угла прямые, является прямоугольником. Например,
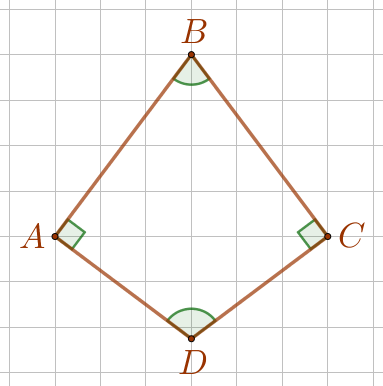 | \(\displaystyle \angle A =90^{\circ}{\small,}\) \(\displaystyle \angle C= 90^{\circ}{\small,}\) \(\displaystyle \angle B \,\cancel=\, 90^{\circ}{\small,}\) \(\displaystyle \angle D \,\cancel=\, 90^{\circ}{\small.}\) \(\displaystyle ABCD\) – не прямоугольник. |
Следовательно, данное утверждение неверно.
Ответ: Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.