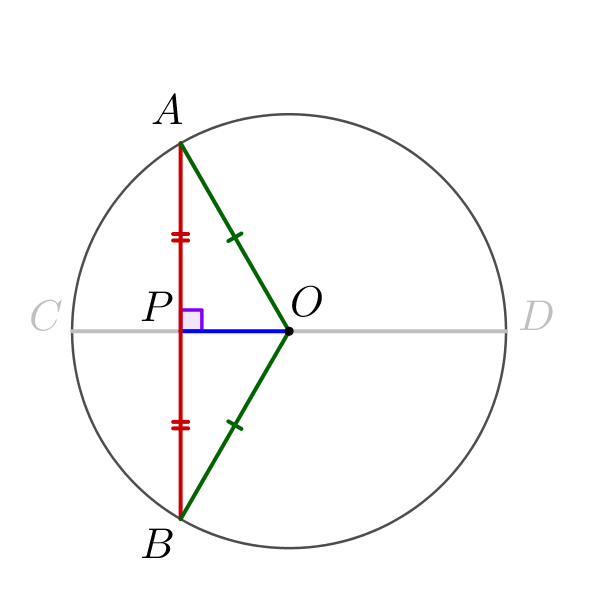
Хорда \(\displaystyle AB\small\) перпендикулярна диаметру \(\displaystyle CD\) окружности радиуса \(\displaystyle 5\small.\) Найдите длину хорды \(\displaystyle AB\small,\) если она делит \(\displaystyle CD\) в отношении \(\displaystyle 1:3\small.\)
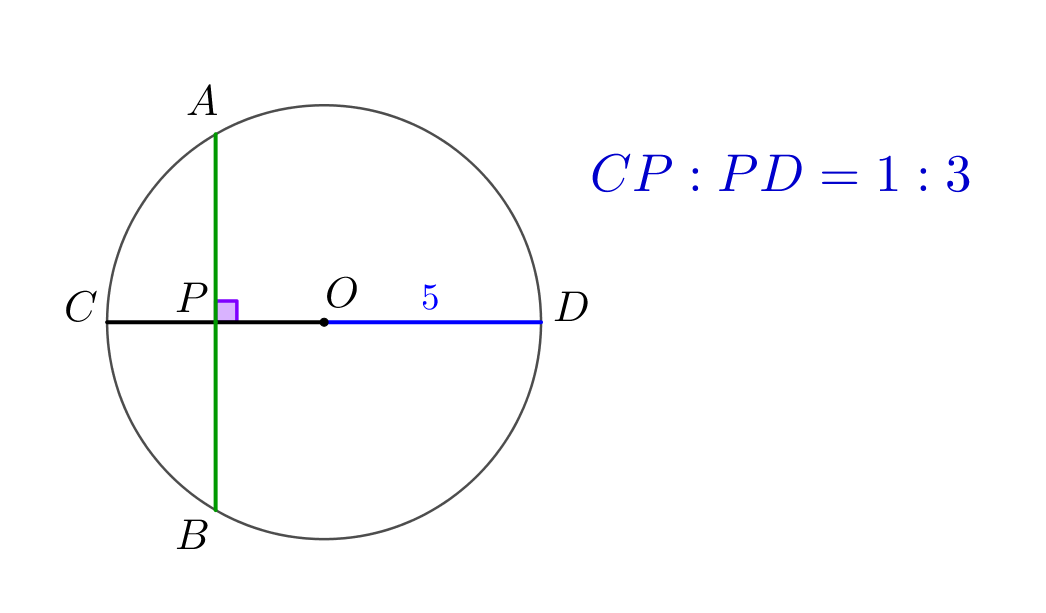
Пусть пересечение хорды \(\displaystyle AB\) и диаметра \(\displaystyle CD\) – точка \(\displaystyle P\small.\) Вписанные углы, опирающиеся на одну дугу окружности, равны. Отметим равные углы: \(\displaystyle \angle CAB=\angle CDB\) и \(\displaystyle \angle ACD=\angle ABD\small.\)
Тогда треугольники \(\displaystyle APC\) и \(\displaystyle DPB\) подобны по двум углам. Значит, выполняется равенство: \(\displaystyle \frac{AP}{DP}=\frac{CP}{BP}\small.\) | 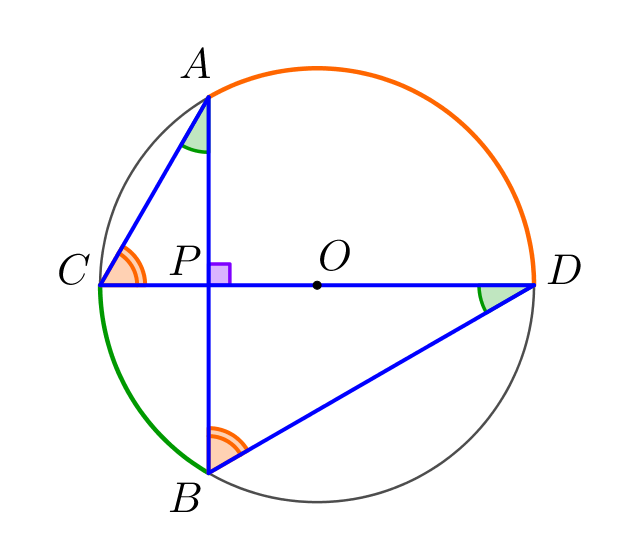 |
Поскольку радиус окружности равен \(\displaystyle 5\small,\) то диаметр \(\displaystyle CD=5\cdot2=10\small.\)
\(\displaystyle CP=\frac{10}{4}=2{,}5\) и \(\displaystyle DP=\frac{10\cdot3}{4}=7{,}5\small.\)
\(\displaystyle AP=BP\small.\)
Подставляя полученные значения в пропорцию, получаем:
\(\displaystyle \frac{AP}{7{,}5}=\frac{2{,}5}{AP}\small,\)
\(\displaystyle AP^2=7{,}5\cdot2{,}5\small.\)
Поскольку длина стороны неотрицательная, то
\(\displaystyle AP=\sqrt{7{,}5\cdot2{,}5}=2{,}5\sqrt{3}\small.\)
Тогда
\(\displaystyle AB=2AP=2\cdot2{,}5\sqrt{3}=5\sqrt{3}\small.\)
Ответ: \(\displaystyle AB=5\sqrt{3}\small.\)