Через точку \(\displaystyle M\small,\) лежащую внутри окружности радиуса \(\displaystyle 5\) с центром \(\displaystyle O\small,\) провели хорду \(\displaystyle AB\small.\) Найдите \(\displaystyle MA\small,\) если \(\displaystyle MB=5\) и \(\displaystyle OM=3\small.\)
Проведем диаметр \(\displaystyle CD\) через точку \(\displaystyle M\small.\) Поскольку радиус окружности равен \(\displaystyle 5\small,\) то
| 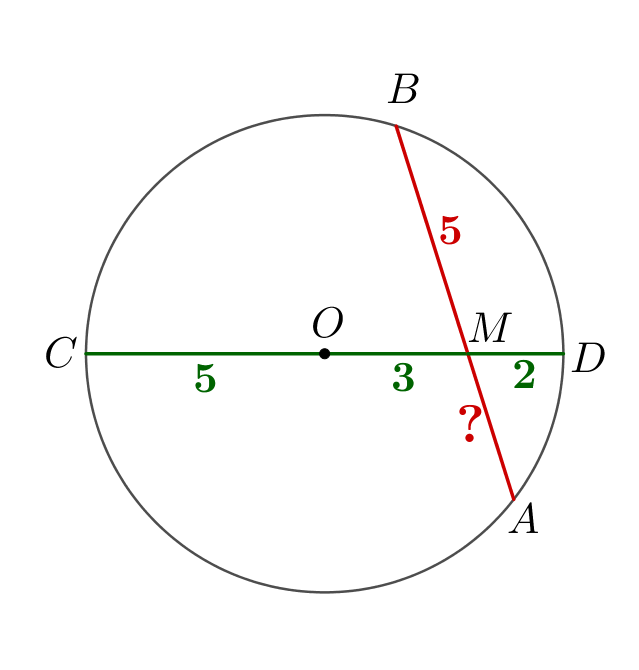 |
Вписанные углы, опирающиеся на одну дугу окружности, равны. Отметим равные углы: \(\displaystyle \angle DAB=\angle DCB\) и \(\displaystyle \angle ADC=\angle ABC\small.\)
Тогда треугольники \(\displaystyle AMD\) и \(\displaystyle CMB\) подобны по двум углам. Значит, выполняется равенство: \(\displaystyle \frac{AM}{CM}=\frac{DM}{BM}\small.\) | 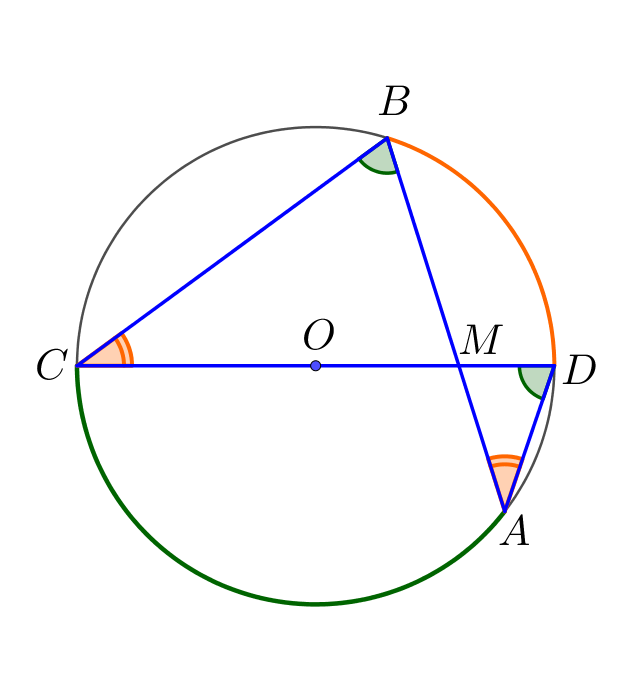 |
Подставляя известные значения \(\displaystyle BM=5,\,CM=8,\,DM=2\small,\) получаем:
\(\displaystyle \frac{AM}{8}=\frac{2}{5}\small,\)
\(\displaystyle AM=\frac{8\cdot2}{5}=3{,}2\small.\)
Ответ: \(\displaystyle AM=3{,}2\small.\)
Отметим, что в процессе решения мы получили:
\(\displaystyle \frac{AM}{CM}=\frac{DM}{BM}\small.\)
Значит, справедливо правило:
Теорема об отрезках пересекающихся хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды:
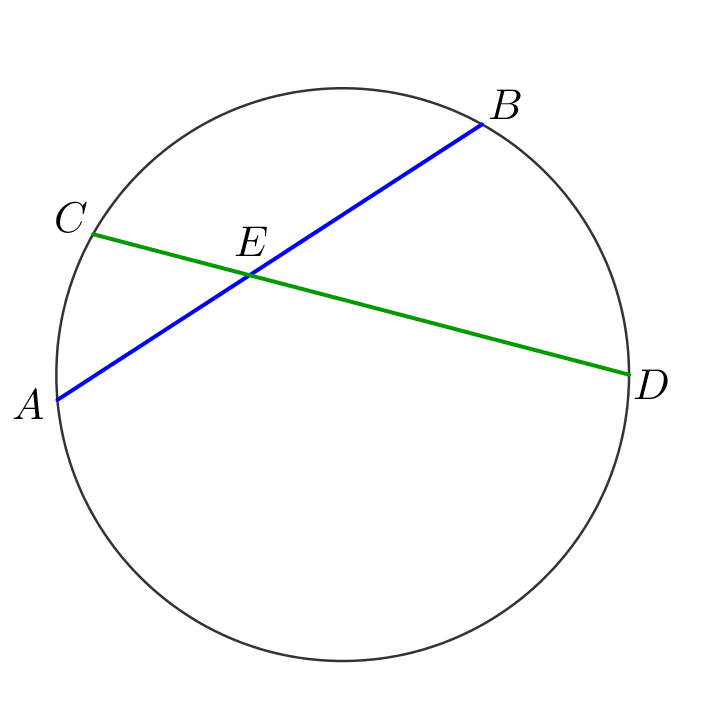
\(\displaystyle \color{blue}{AE}\cdot \color{blue}{BE}=\color{green}{CE}\cdot \color{green}{ DE}\)