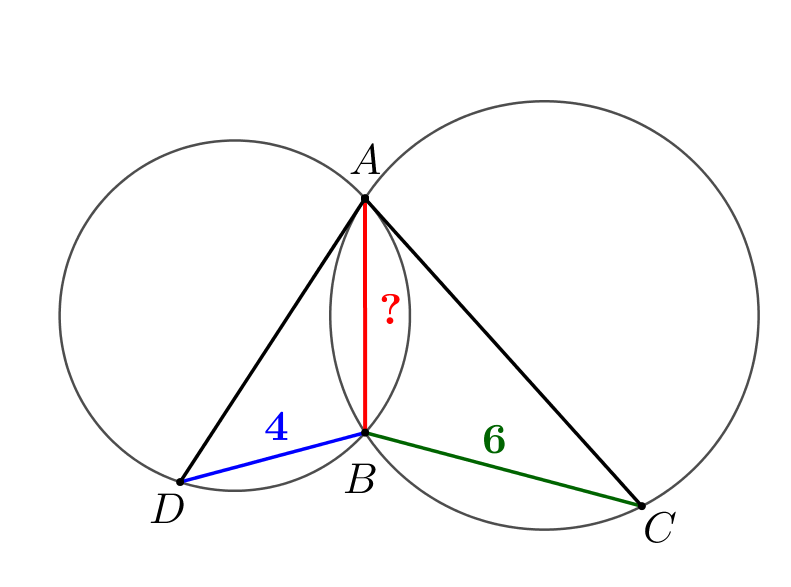
Две окружности пересекаются в точках \(\displaystyle A\) и \(\displaystyle B\small.\) Проведены хорды \(\displaystyle AC\) и \(\displaystyle AD\) этих окружностей так, что хорда одной окружности касается другой окружности. Найдите \(\displaystyle AB\small,\) если \(\displaystyle CB = 6,\, DB = 4\small.\)
Чтобы найти равные углы, воспользуемся правилом:
Угол между хордой и касательной равен вписанному углу, опирающемуся на данную хорду.
\(\displaystyle \angle ABD=\angle ACB\small.\) | 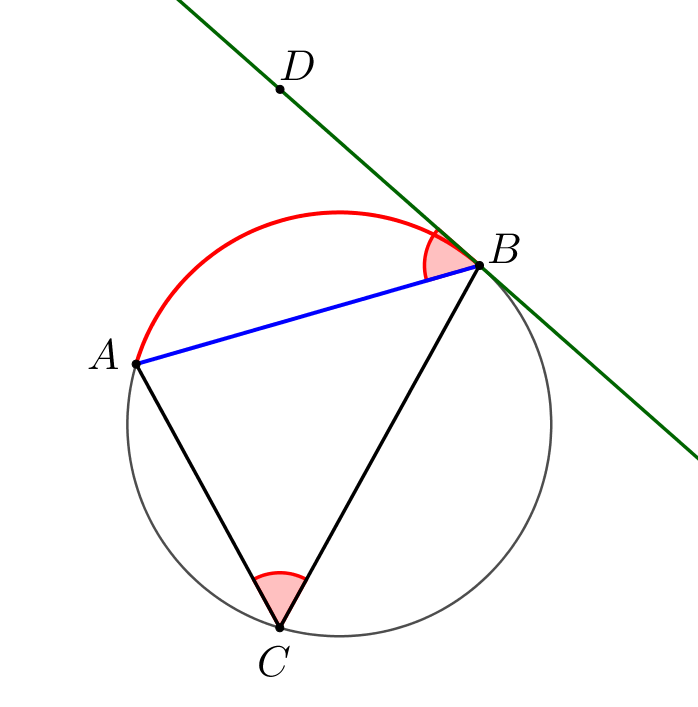 |
Получаем:
| 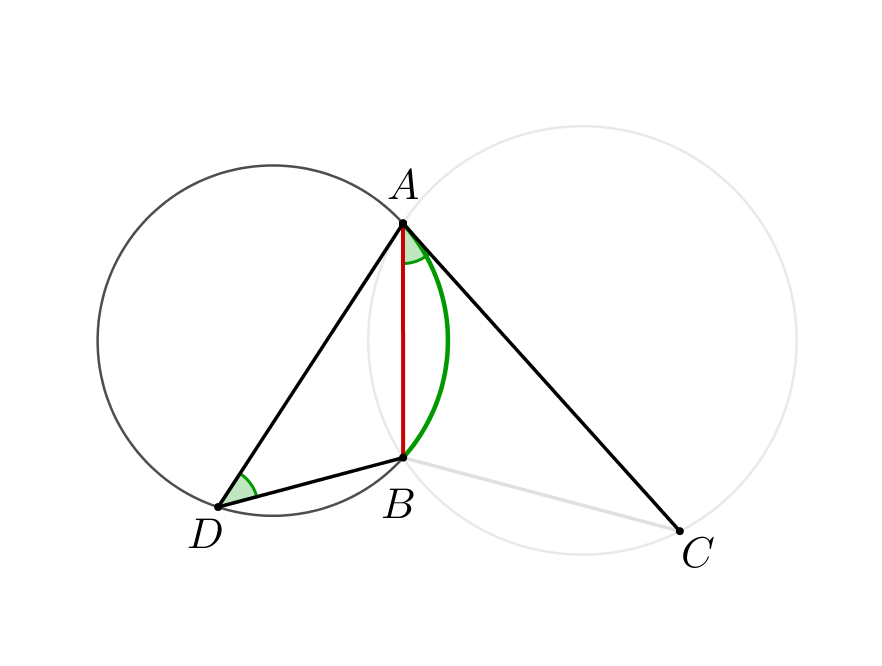 |
| 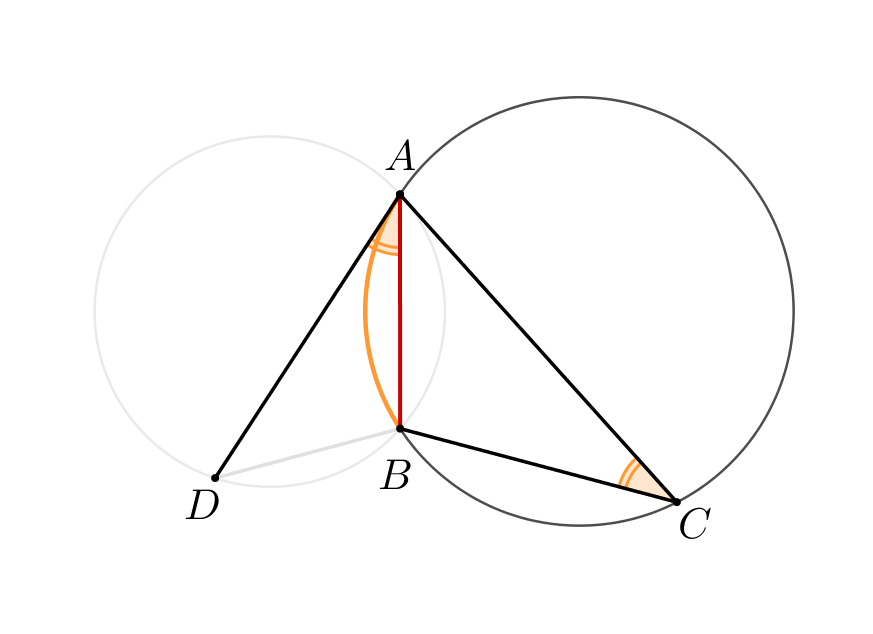 |
Тогда треугольники \(\displaystyle CAB\) и \(\displaystyle ADB\) подобны по двум углам. Получаем: \(\displaystyle \frac{CB}{AB}=\frac{AB}{BD}\small.\)
\(\displaystyle \frac{6}{AB}=\frac{AB}{4}\small,\) \(\displaystyle AB^2=6\cdot4\small.\) | 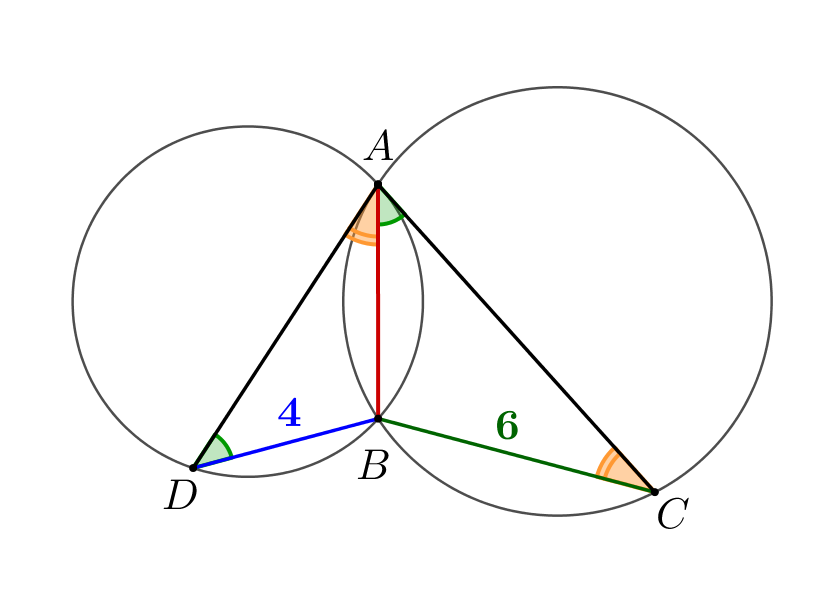 |
Длина стороны неотрицательное число, значит,
\(\displaystyle AB=\sqrt{6\cdot4}=2\sqrt{6}\small.\)
Ответ: \(\displaystyle AB=2\sqrt{6}\small.\)