В окружности проведены хорды \(\displaystyle AB\) и \(\displaystyle CD\small,\) пересекающиеся в точке \(\displaystyle M\small.\) Точка \(\displaystyle L\) – точка пересечения биссектрисы угла \(\displaystyle BMD\) с хордой \(\displaystyle BD\small.\) Найдите отрезки \(\displaystyle BL\) и \(\displaystyle LD\small,\) если \(\displaystyle BD=8\small,\) а площади треугольников \(\displaystyle CMB\) и \(\displaystyle AMD\) относятся как \(\displaystyle 1:4\small.\)
\(\displaystyle S_{CMB}:S_{AMD}=1:4\small.\)
Чтобы решить задачу:
| 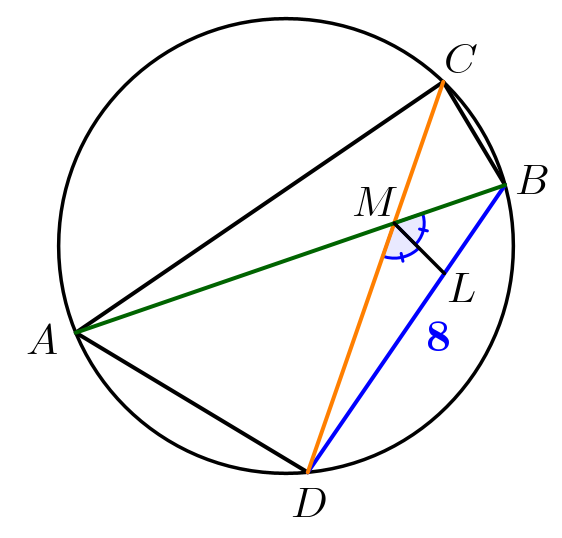 |
\(\displaystyle DM:BM=2:1\small.\)
Вписанные углы, опирающиеся на одну дугу окружности, равны. Отметим равные углы: \(\displaystyle \angle DAB=\angle DCB\) и \(\displaystyle \angle ADC=\angle ABC\small.\) Тогда треугольники \(\displaystyle AMD\) и \(\displaystyle CMB\) подобны по двум углам. Значит, отношение сторон равно коэффициенту подобия \(\displaystyle k=\frac{DM}{BM}\small,\) а отношение площадей равно квадрату коэффициента подобия: \(\displaystyle k^2=\frac{S_{AMD}}{S_{CMB}}=4\small.\) Тогда \(\displaystyle k=\sqrt{4}=2\) и \(\displaystyle \frac{DM}{BM}=k=2\small.\) | 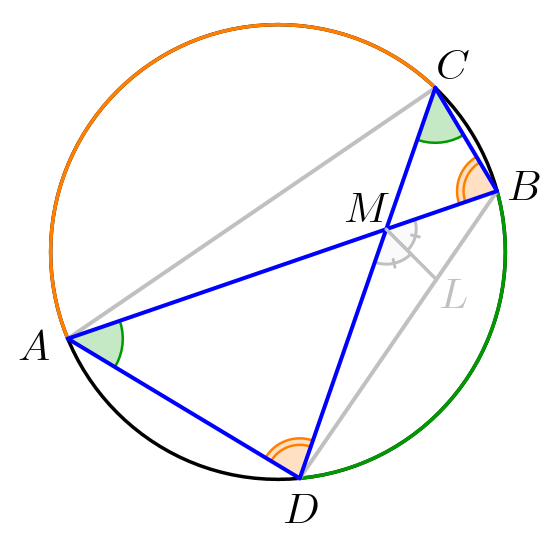 |
Поскольку \(\displaystyle ML\) – биссектриса треугольника \(\displaystyle BMD\small,\) то по свойству биссектрисы:
\(\displaystyle \frac{DL}{BL}=\frac{DM}{BM}=2\small.\)
По условию, \(\displaystyle BD=8\small.\)
\(\displaystyle DL=8\cdot\frac{2}{3}=\frac{16}{3}\) и \(\displaystyle BL=8\cdot\frac{1}{3}=\frac{8}{3}\small.\)
Ответ: \(\displaystyle BL=\frac{8}{3}\) и \(\displaystyle DL=\frac{16}{3}\small.\)