Четырехугольник \(\displaystyle ABCD\) вписан в окружность. Диагональ \(\displaystyle AC\) является биссектрисой угла \(\displaystyle BAD\) и пересекается с диагональю \(\displaystyle BD\) в точке \(\displaystyle K\small.\) Найдите \(\displaystyle KC\small,\) если \(\displaystyle BC = 4\) и \(\displaystyle AK = 6\small.\)
\(\displaystyle AC\) – биссектриса угла \(\displaystyle BAD\small,\) тогда \(\displaystyle \angle BAC=\angle DAC\small.\) Вписанные углы, опирающиеся на одну дугу окружности, равны. Отметим равные углы:
| 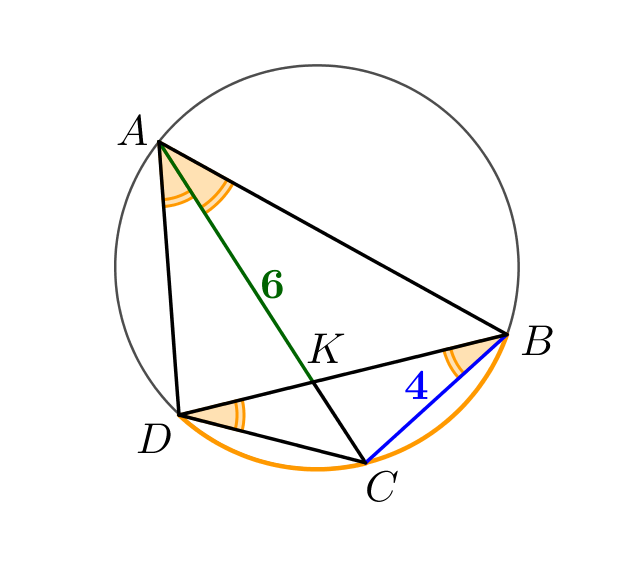 |
Треугольники \(\displaystyle ABC\) и \(\displaystyle BKC\) подобны по двум углам: \(\displaystyle \angle CAB=\angle CBK\) и \(\displaystyle \angle ACB=\angle BCK\small.\) Тогда \(\displaystyle \frac{AC}{BC}=\frac{BC}{KC}\small.\)
\(\displaystyle AC=AK+KC=6+x\small.\) | 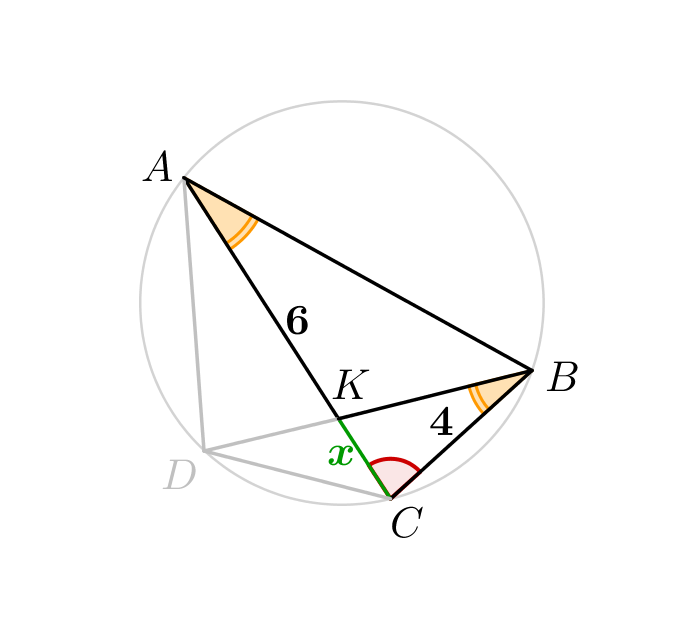 |
Подставим соответствующие значения в пропорцию:
\(\displaystyle \frac{6+x}{4}=\frac{4}{x}\small.\)
Упростим выражение
\(\displaystyle (6+x)x=4\cdot4\small,\)
\(\displaystyle x^2+6x-16=0\small.\)
\(\displaystyle x=2\) или \(\displaystyle x=-8\small.\)
Длина стороны неотрицательное число, значит,
\(\displaystyle KC=x=2\small.\)
Ответ: \(\displaystyle KC=2\small.\)