Изображённые отрезки с обозначенными концами образуют геометрические фигуры.
Рассмотрим каждую такую фигуру и выберем те из них, которые соответствуют определению ломаной.
Вспомним определение ломаной
ломаная и ее элементыЛоманой называется геометрическая фигура, состоящая из нескольких следующих друг за другом отрезков. При этом:
- каждые два соседних отрезка последовательности имеют общий конец, но не лежат на одной прямой;
- оба конца каждого отрезка могут быть концами только разных из соседних с ним отрезков.
Концы отрезков называются вершинами ломаной, а сами отрезки — звенья ломаной.
Соседние в последовательности звенья называются смежными.
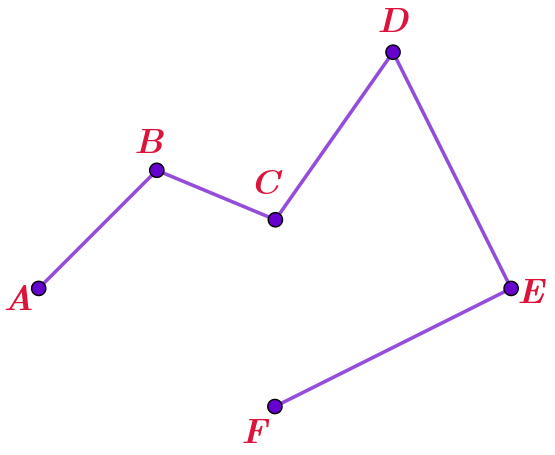
На рисунке изображена ломаная \(\displaystyle ABCDEF{\small .}\)
- точки \(\displaystyle A,\,B,\,C,\,D,\,E,\,F\)— вершины ломаной;
- отрезки \(\displaystyle AB,\,BC,\,CD,\,DE,\,EF\)— звенья ломаной, перечисленные в последовательности, соответствующей определению.
Вершины \(\displaystyle A\) и \(\displaystyle F\)— принадлежат только одному звену каждая. Такие вершины называют концами ломаной.
Из определения следует, что у ломаной не может быть больше двух концов.
Чтобы доказать, что состоящая из отрезков фигура является ломаной, нужно "собрать" отрезки в последовательность, соответствующую определению.
Попробуем это сделать для каждой данной фигуры.
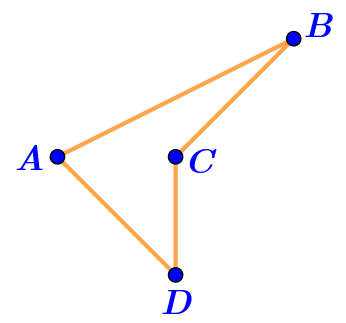
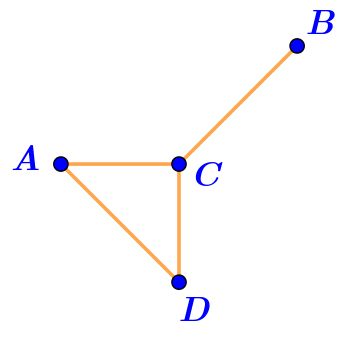
Фигура на рисунке \(\displaystyle \rm I\) — ломаная.
Отрезки \(\displaystyle AB,\,BC,\,CD,\,AD\) последовательно соединены своими концами и никакие два смежных отрезка не лежат на одной прямой.
Значит, фигура на рисунке \(\displaystyle \rm I\) — ломаная \(\displaystyle ABCD{\small .}\)
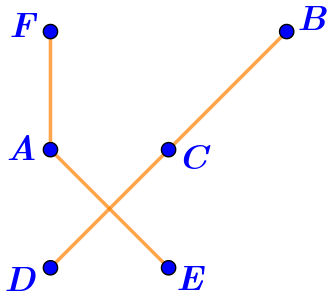
Фигура на рисунке \(\displaystyle \rm II\) не является ломаной.
Если бы эта фигура была ломаной, то она имела бы четыре конца.
Это невозможно: концы ломаной должны быть концами первого и последнего звеньев.
На рисунке же это концы четырёх разных отрезков.
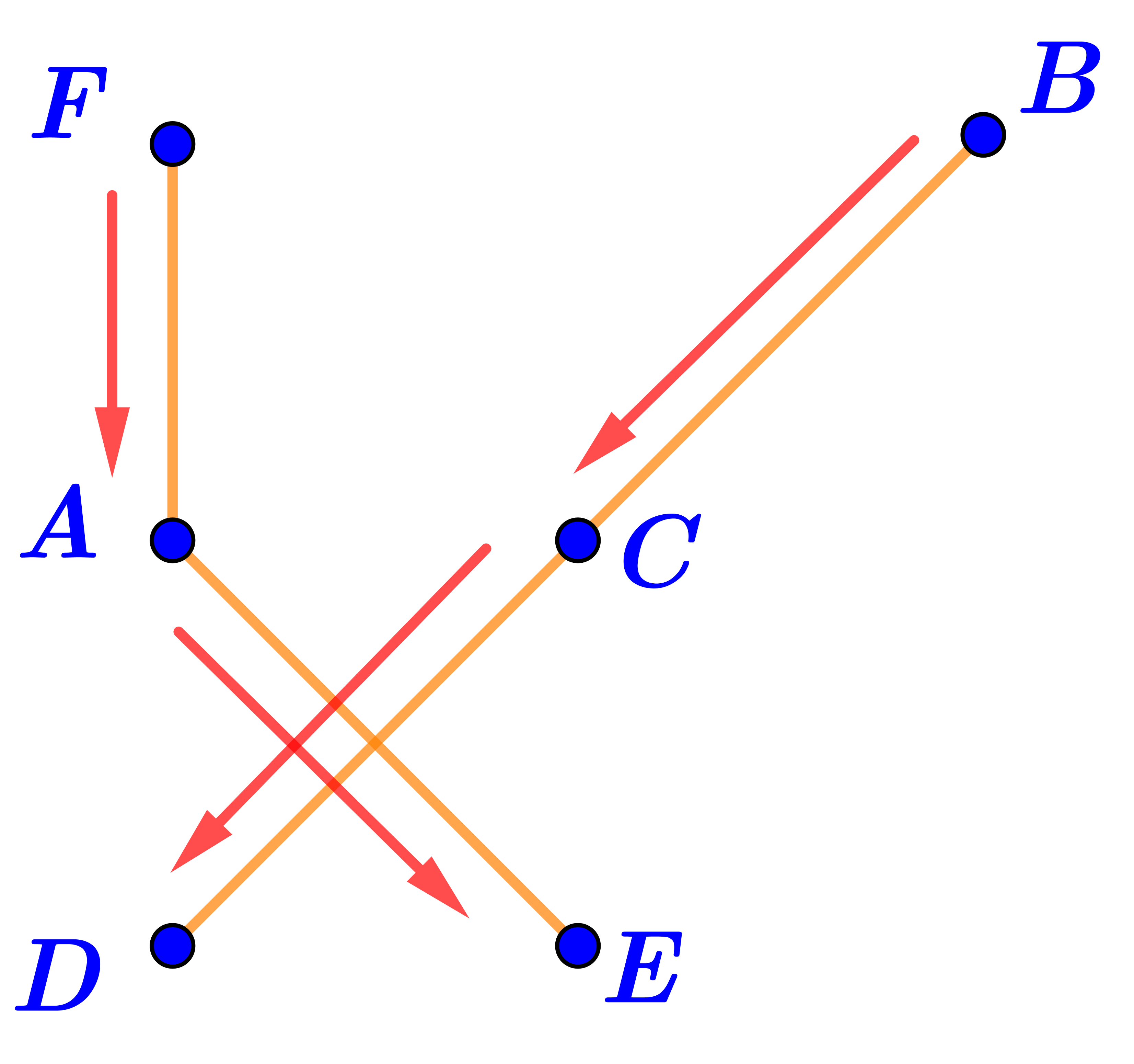
Получается, на рисунке не одна, а минимум две ломаных.
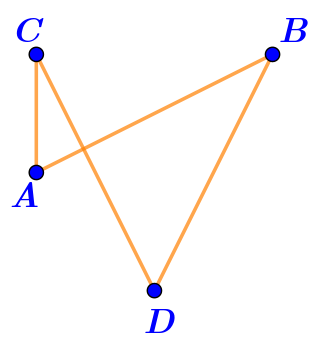
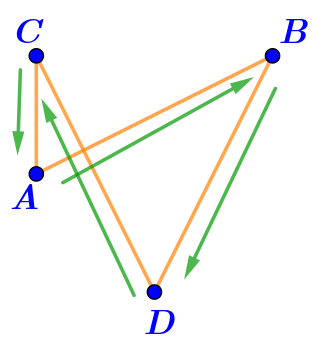
Фигура на рисунке \(\displaystyle \rm III\) — ломаная.
Отрезки \(\displaystyle CA,\,AB,\,BD,\,DC\) последовательно соединены своими концами и никакие два смежных отрезка не лежат на одной прямой.
Значит, фигура на рисунке \(\displaystyle \rm III\) — ломаная \(\displaystyle CABD{\small .}\)
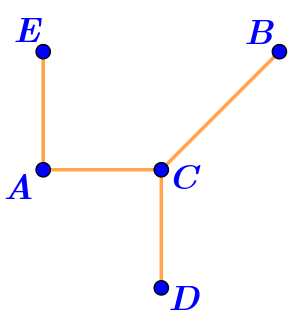
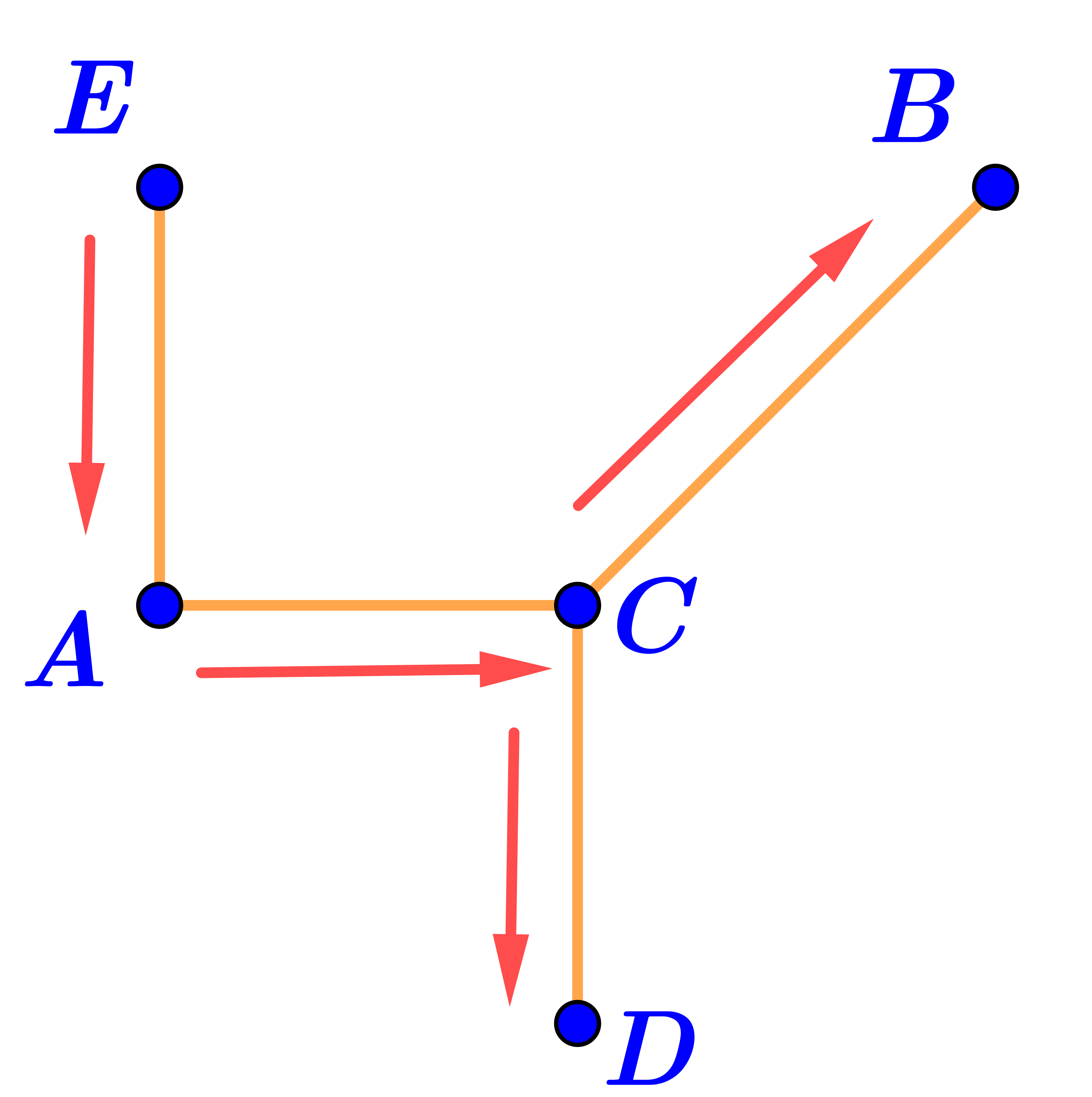
Фигура на рисунке \(\displaystyle \rm IV\) не является ломаной.
Отрезки \(\displaystyle AE{\small ,\;}BC\) и \(\displaystyle CD\) могли бы быть только крайними звеньями ломаной. Но их три, а крайних звеньев не может быть больше двух.
Значит, фигура на рисунке \(\displaystyle \rm IV\) не является ломаной.
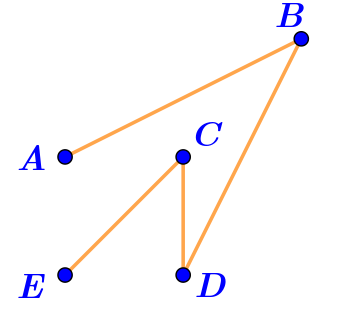
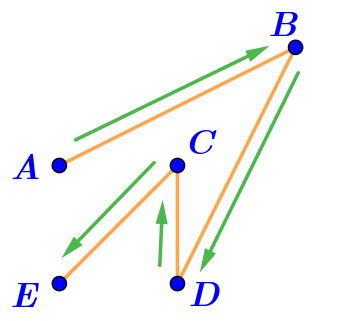
Фигура на рисунке \(\displaystyle \rm V\) — ломаная.
Отрезки \(\displaystyle AB,\,BD,\,DC,\,CE\) последовательно соединены своими концами и никакие два смежных отрезка не лежат на одной прямой.
Значит, фигура на рисунке \(\displaystyle \rm V\) — ломаная \(\displaystyle ABDCE{\small .}\) .
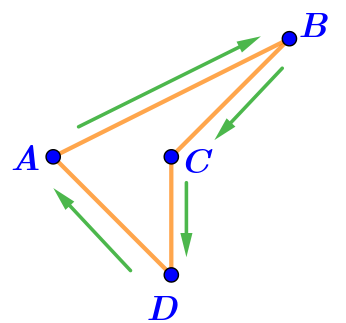
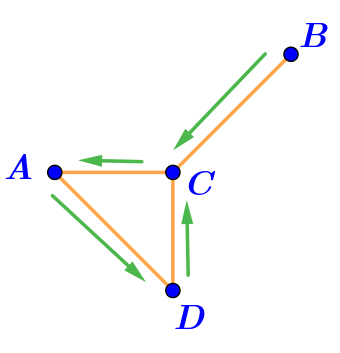
Фигура на рисунке \(\displaystyle \rm VI\) — ломаная.
Отрезки \(\displaystyle BC,\,CA,\,AD,\,DC\) последовательно соединены своими концами и никакие два смежных отрезка не лежат на одной прямой.
Значит, фигура на рисунке \(\displaystyle \rm VI\) — ломаная \(\displaystyle BADC{\small .}\)
Ответ: фигуры \(\displaystyle \rm I,\,III,\,V,\,VI{\small .}\)