На каждом из рисунков изображена ломаная из шести звеньев.
\(\displaystyle ~~~\large\rm I{\small .}\)
| 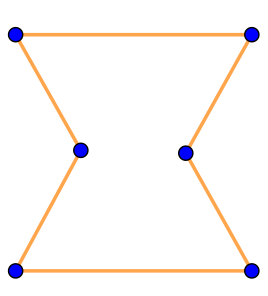 | \(\displaystyle ~~~~\large\rm II{\small .}\) | 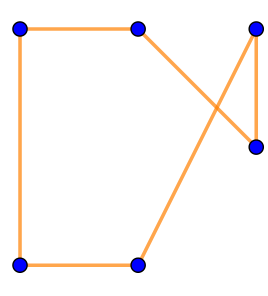 | \(\displaystyle ~~\large\rm III{\small .}\) | 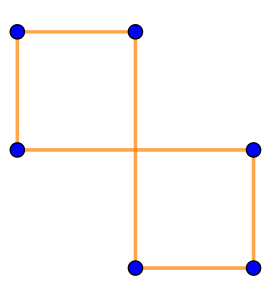 |
| \(\displaystyle ~~~\large\rm IV{\small .}\) | 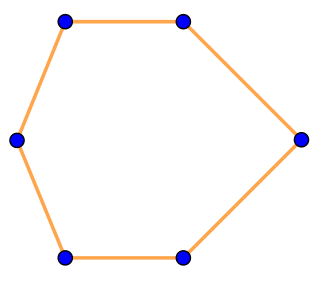 | \(\displaystyle ~~~~\large\rm V{\small .}\) | 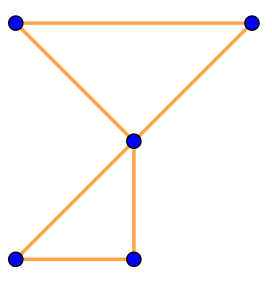 | \(\displaystyle ~~\large\rm VI{\small .}\) | 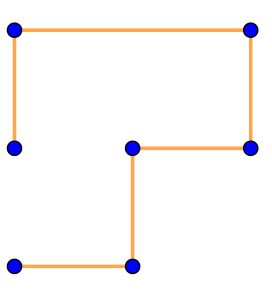 |
На каких из рисунков изображённая ломаная линия является многоугольником?
Последовательно рассмотрим каждую ломаную на соответствие определению многоугольника.
Многоугольником называется замкнутая ломаная, несмежные звенья которой не имеют общих точек.
Вершины этой ломаной называют вершинами многоугольника, звенья ломаной — сторонами многоугольника.
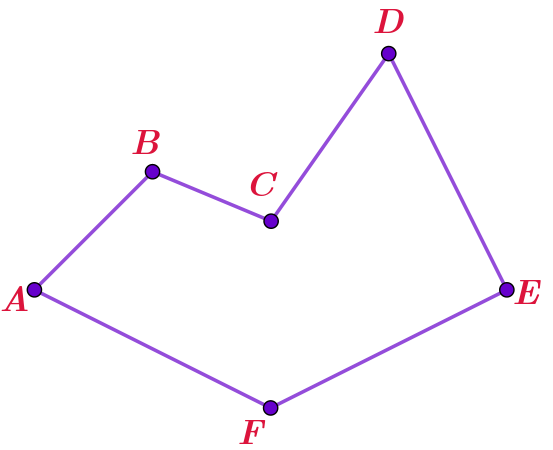
На рисунке изображен многоугольник \(\displaystyle ABCDEF{\small .}\) В нем:
- точки \(\displaystyle A,\,B,\,C,\,D,\,E,\,F\) — вершины многоугольника;
- отрезки \(\displaystyle AB,\,BC,\,CD,\,DE,\,EF,\,FA\) — стороны многоугольника.
Каждая сторона многоугольника соединяет две вершины, каждая вершина принадлежит двум сторонам.
Это означает, что число вершин многоугольника всегда равно числу его сторон.
По этому числу \(\displaystyle n\) многоугольник называют \(\displaystyle n\)-угольником.
На рисунке, например, изображён шестиугольник.
Из определения следует, что многоугольник – это такая замкнутая ломаная, которая не имеет самопересечений.
| РИСУНОК | ЧЕРТЁЖ | ВЫВОД |
| \(\displaystyle \rm I\) | 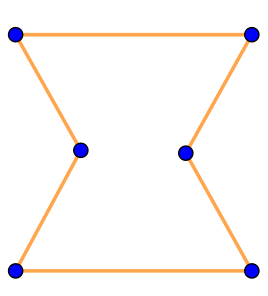 | Ломаная замкнута, общие точки имеют только смежные звенья. Значит, на рисунке \(\displaystyle \rm I\) изображён многоугольник |
| \(\displaystyle \rm II\) | 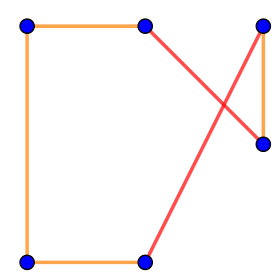 | Ломаная замкнута, но два выделенных на рисунке звена имеют общую внутреннюю точку. Значит, на рисунке \(\displaystyle \rm II\) изображен не многоугольник |
| \(\displaystyle \rm III\) | 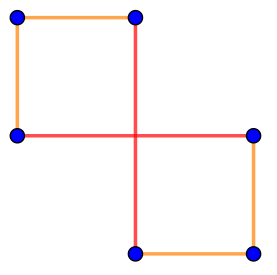 | Ломаная замкнута, но два выделенных на рисунке звена имеют общую внутреннюю точку. Значит, на рисунке \(\displaystyle \rm III\) изображен не многоугольник |
| \(\displaystyle \rm IV\) | 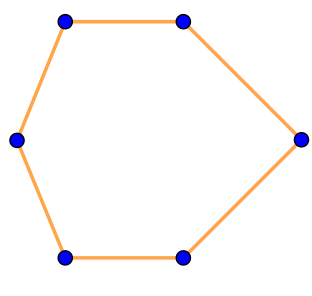 | Ломаная замкнута, общие точки имеют только смежные звенья. Значит, на рисунке \(\displaystyle \rm IV\) изображён многоугольник |
| \(\displaystyle \rm V\) | 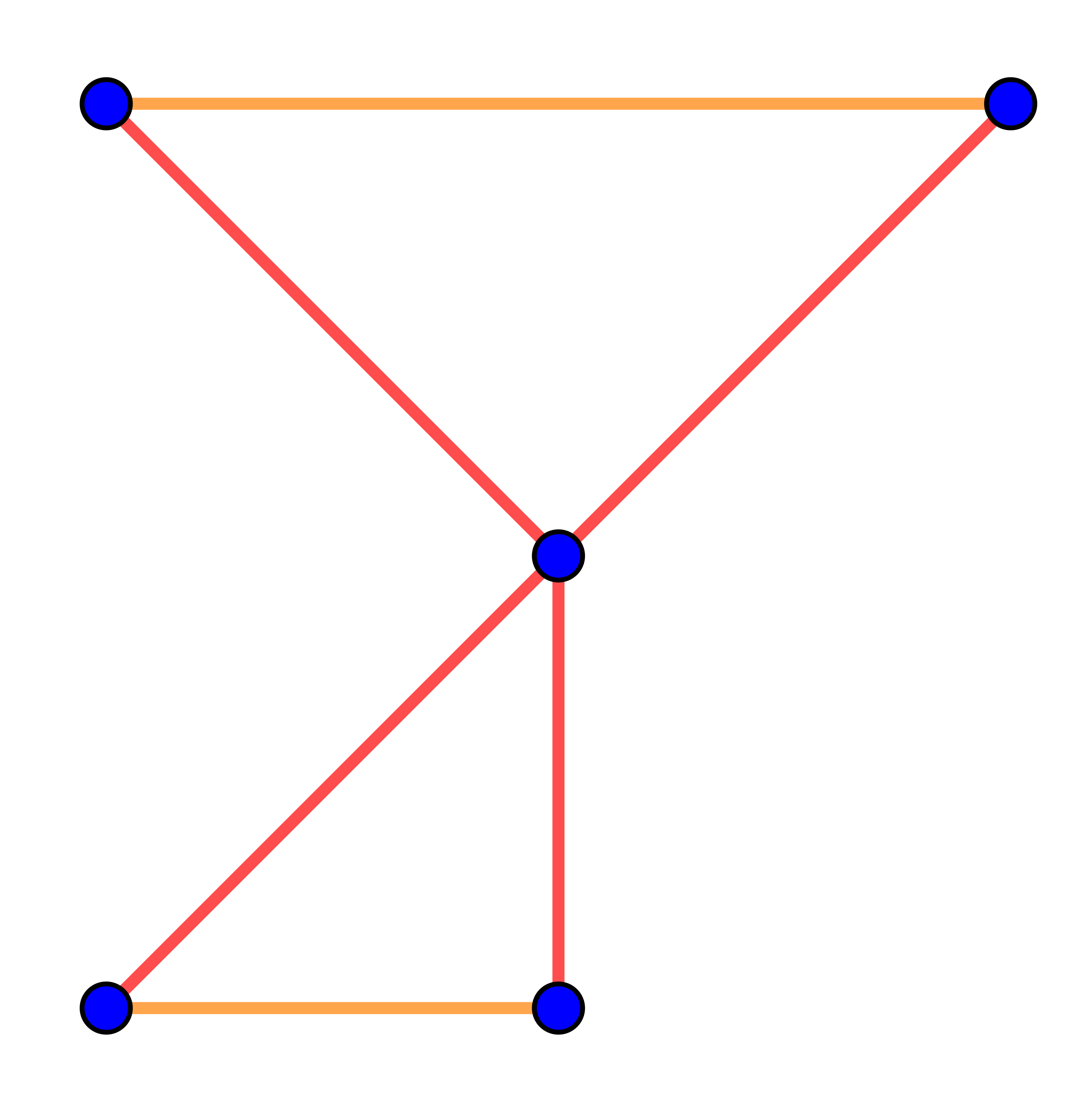 | Ломаная замкнута, но одна из её вершим принадлежит сразу четырём звеньям (даже среди трёх звеньев всегда есть пара несмежных). Значит, на рисунке \(\displaystyle \rm V\) изображен не многоугольник |
| \(\displaystyle \rm VI\) | 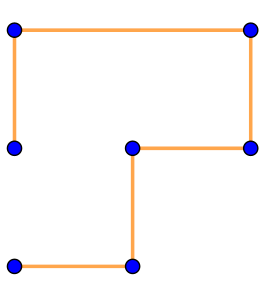 | Ломаная не является замкнутой. Значит, на рисунке \(\displaystyle \rm VI\) изображен не многоугольник |
Ответ: многоугольниками являются фигуры \(\displaystyle \rm I,IV{\small .}\)