Боковая сторона равнобедренной трапеции равна \(\displaystyle 8{\small,}\) периметр данной трапеции \(\displaystyle 31{\small,}\) одно из оснований равно \(\displaystyle 7{\small.}\) Найдите длину другого основания трапеции.
Трапеция называется равнобедренной, если её боковые стороны равны. |  |
Пусть \(\displaystyle ABCD\) – равнобедренная трапеция:
Требуется найти основание \(\displaystyle AD{\small.}\) | 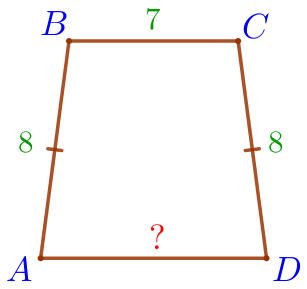 |
Периметр многоугольника равен сумме длин всех его сторон. Тогда
\(\displaystyle P_{ABCD}=AB+BC+CD+AD{\small.}\)
Подставим известные величины:
\(\displaystyle 31=8+7+8+AD{\small,}\)
\(\displaystyle 31=23+AD{\small.}\)
Получаем:
\(\displaystyle AD=31-23=8{\small.}\)
Ответ: \(\displaystyle 8{\small.}\)