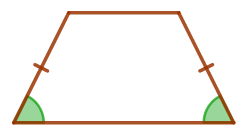
В равнобедренной трапеции \(\displaystyle ABCD\) диагональ \(\displaystyle AC\) равна \(\displaystyle 5{\small.}\) Найдите диагональ \(\displaystyle BD{\small.}\)
\(\displaystyle BD=\)
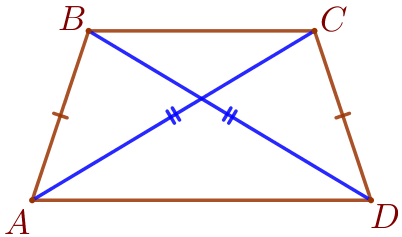
\(\displaystyle ABCD\) – равнобедренная трапеция:
Требуется найти диагональ \(\displaystyle BD{\small.}\) | 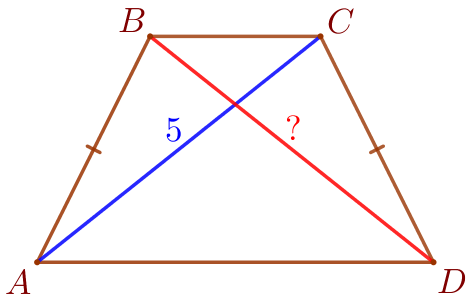 |
\(\displaystyle \angle BAD=\angle CDA{\small.}\)
Рассмотрим треугольники \(\displaystyle BAD\) и \(\displaystyle CDA{\small.}\)
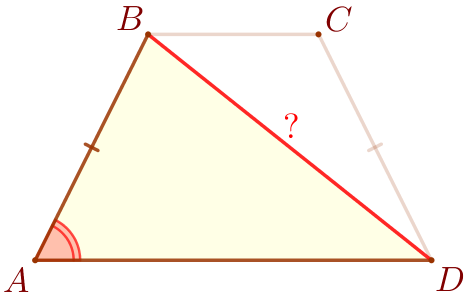 | 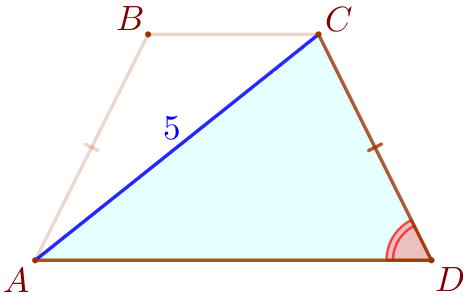 |
| |
Следовательно,
\(\displaystyle \triangle BAD=\triangle CDA\) – по двум сторонам и углу между ними.
Значит, стороны \(\displaystyle BD\) и \(\displaystyle AC\) равны:
\(\displaystyle BD=AC=5{\small.}\)
Ответ: \(\displaystyle BD=5{\small.}\)
Из равенства треугольников \(\displaystyle ABD\) и \(\displaystyle ACD\) следует:
Диагонали равнобедренной трапеции равны:
\(\displaystyle AC = BD\small.\)