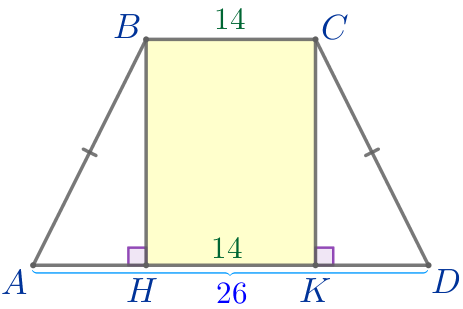
В равнобедренной трапеции \(\displaystyle ABCD\) основания \(\displaystyle BC\) и \(\displaystyle AD\) равны соответственно \(\displaystyle 14\) и \(\displaystyle 26{\small.}\) Высоты \(\displaystyle BH\) и \(\displaystyle CK\) делят большее основание на три отрезка. Найдите длину меньшего из полученных отрезков.
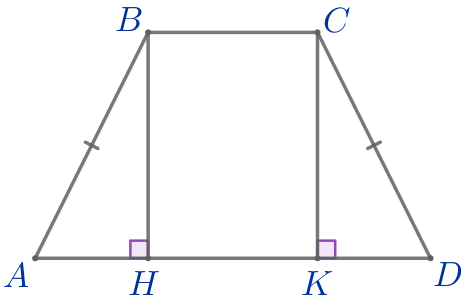
\(\displaystyle ABCD\) – равнобедренная трапеция:
|  |
Требуется найти наименьший из отрезков \(\displaystyle AH{\small,}\) \(\displaystyle HK\) и \(\displaystyle KD{\small.}\)
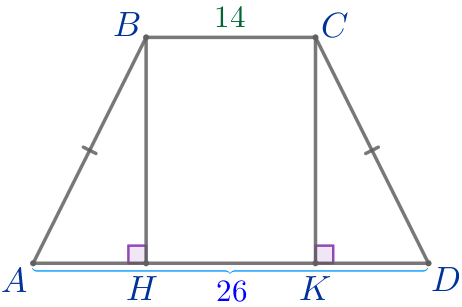
\(\displaystyle HK=BC=14{\small.}\)
\(\displaystyle \angle BAD=\angle CDA{\small.}\)
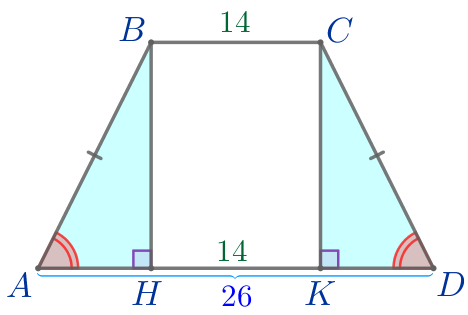 |
Следовательно, \(\displaystyle \triangle ABH= \triangle DCK\) по гипотенузе и острому углу. |
Значит, равны катеты \(\displaystyle AH\) и \(\displaystyle KD{\small,}\) то есть
\(\displaystyle AH=KD=\frac{AD-HK}{2}{\small;}\)
\(\displaystyle AH=KD=\frac{26-14}{2}=\frac{12}{2}=6{\small.}\)
Получили:
\(\displaystyle AH=6{\small;}\) \(\displaystyle HK=14{\small;}\) \(\displaystyle KD=6{\small.}\)
Так как \(\displaystyle 6<14{\small,}\) то длина меньшего из полученных отрезков равна \(\displaystyle 6{\small.}\)
Ответ: \(\displaystyle 6{\small.}\)