Две равные по длине хорды \(\displaystyle AB\) и \(\displaystyle CD\) пересекаются в точке \(\displaystyle E\small.\) Найдите \(\displaystyle AE\) и \(\displaystyle BE\small,\) если \(\displaystyle CE=4,\,DE=6\) и \(\displaystyle AE<BE\small.\)
Воспользуемся правилом
Теорема об отрезках пересекающихся хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды:
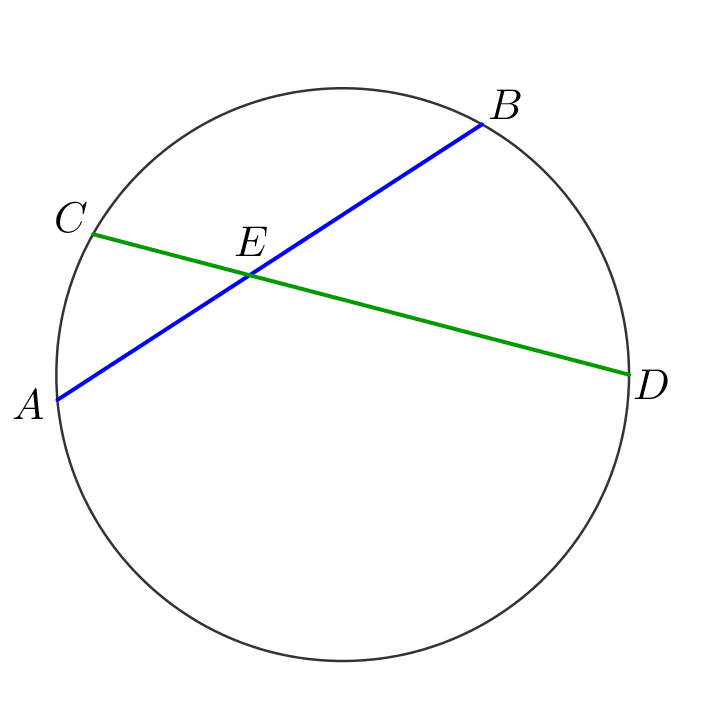
\(\displaystyle \color{blue}{AE}\cdot \color{blue}{BE}=\color{green}{CE}\cdot \color{green}{ DE}\)
Тогда
\(\displaystyle AE\cdot BE=CE\cdot DE\)
Подставим значения \(\displaystyle CE=4,\,DE=6{\small:}\)
\(\displaystyle AE\cdot BE=CE\cdot DE=4\cdot6=24\small.\)
Также из условия
\(\displaystyle AE+BE=AB=CD=4+6=10\small.\)
Решим систему уравнений:
\(\displaystyle \begin{cases}AE\cdot BE=24,\\AE+BE=10.\end{cases}\)
\(\displaystyle AE=4\) и \(\displaystyle BE=6\small.\)
Выразим из второго уравнения \(\displaystyle AE{\small:}\)
\(\displaystyle AE=10-BE\small.\)
Подставляем в первое уравнение:
\(\displaystyle (10-BE)\cdot BE=24\small,\)
\(\displaystyle 10BE-BE^2=24\small,\)
\(\displaystyle BE^2-10BE+24=0\small.\)
Решим получившееся квадратное уравнение
\(\displaystyle x^2-10x+24=0\small.\)
Дискриминант уравнения равен:
\(\displaystyle {\rm D}=10^2-4\cdot24=4\) и \(\displaystyle {\rm \sqrt{D}}=\sqrt{4}=2\small.\)
Тогда корни уравнения:
\(\displaystyle x_1=\frac{10+2}{2}=6\) и \(\displaystyle x_2=\frac{10-2}{2}=4\small.\)
Поскольку по условию \(\displaystyle AE<BE\small,\) то
\(\displaystyle BE=6\) и \(\displaystyle AE=4\small.\)
Ответ: \(\displaystyle AE=4\) и \(\displaystyle BE=6\small.\)
Отметим, что если
- произведение чисел равно \(\displaystyle 24\small,\)
- сумма чисел \(\displaystyle 10\small,\)
то по теореме Виета, эти числа – решения уравнения:
\(\displaystyle x^2-10x+24=0\small.\)
Значит, пара \(\displaystyle (AE;\,BE)\) и пара \(\displaystyle (CE;\,DE)\) являются парой корней квадратного уравнения
\(\displaystyle x^2-10x+24=0\small.\)
Следовательно,
либо \(\displaystyle AE=CE\) и \(\displaystyle BE=DE\small,\)
либо \(\displaystyle AE=DE\) и \(\displaystyle BE=CE\small.\)